Difficulty: Beginner
Prerequisites
- The project requires you to be able to run Python on your computer, but does not require any programming skill.
- This project requires the following Python modules to be installed on your computer:
pygame
Background
Recursion and runtime are two important concepts in computer science. Recursion is a strategy of solving a problem where doing a task involves doing a smaller version of that task, which involves doing an even smaller version of the task … until the task becomes so small that it can be done very easily.
For example, say Bob picked a number from 1 to 100 and Amy’s job is to guess it. Each time Amy guesses, Bob will tell Amy whether her guess is too high or too low. So, if Amy’s first guess is 50, Bob might say “too high.” Now, Amy’s problem is to pick a number from 1 to 49. This is just a smaller version of her first job! This means that Amy doesn’t have to come up with a new strategy for each guess; she can use the same logic for each smaller job, or “level of recursion.” Once Amy has guessed enough that her job is to pick a number from, say, 37 to 37, the job is so small that she doesn’t even need a strategy, and she is done. This is an example of a problem that can be solved using recursion.
Runtime is simply how long a program takes to run. Choosing a different strategy, or “algorithm,” can make a program run much faster or slower.
Measuring Runtime Scaling
The King of Programmia wants to create a new national flag. He was recently introduced to the idea of fractals, so he got one of his advisors to write a program to draw a Sierpinski triangle. The program is recursive and lets the user decide how many levels they want to draw. Two levels looks like this:
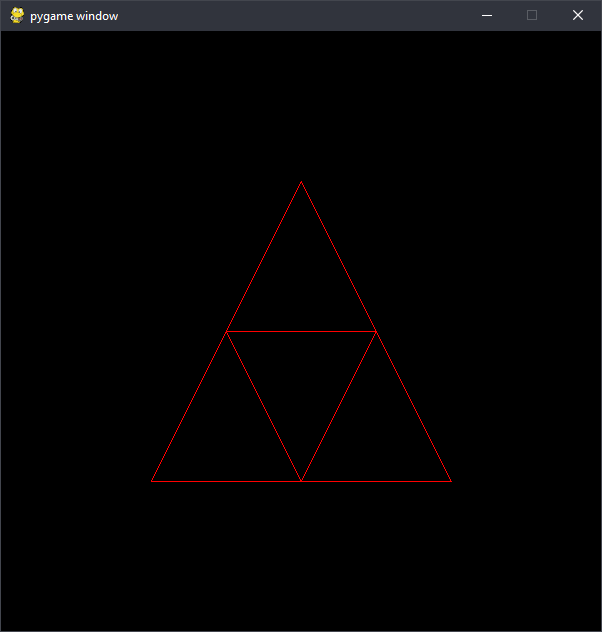
while four levels look like this:
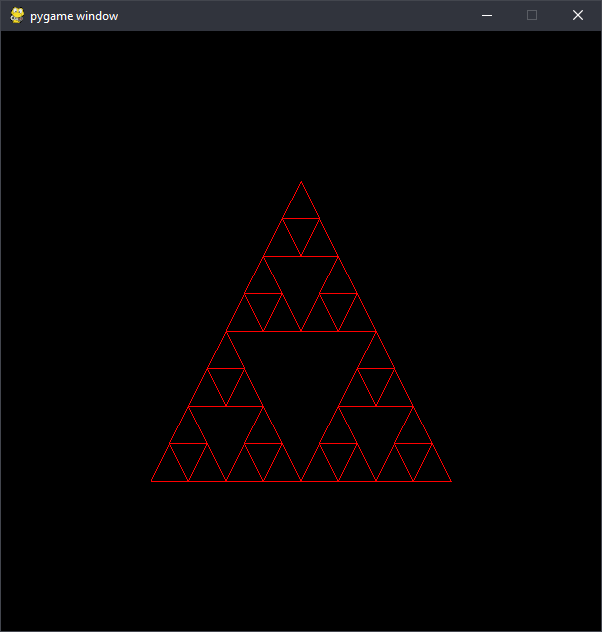
The King wanted the coolest-looking Sierpinski triangle possible, so he asked the program for 20 levels. After waiting for a full minute without the program finishing, he quit it and threatened to throw the writer in the dungeons for giving him a broken program. The writer of the program has asked you to go to the king for him and explain why the program can’t draw 20 levels in a reasonable amount of time, even though drawing 5 levels takes less than a tenth of a second.
You decide you need some data.
What to Do
- Download
triangle_recursive.pyfrom here. - Run the program. It will prompt you for a number of iterations (levels to draw). Enter a low number, like 5.
- The program should open a window with the Sierpinski triangle drawn, like the ones shown above. Going back to the text prompt, there should be a runtime in seconds – how long the computer took to draw the triangle. (Times below 0.001 seconds might be displayed as 0.0 seconds, just because the clock is only so precise). Record this time in a spreadsheet (like Google Sheets or Microsoft Excel).
- Record the time taken for each number from 5 iterations to 15 iterations. For extra accuracy, do each number of iterations a few times and average the results. The later ones may take a few seconds to complete.
- Use your spreadsheet software to graph your data as points (scatter plot), with the number of iterations on the x-axis and the runtime on the y-axis. Try to fit your data with a linear, quadratic, and exponential curve. Which fits best?

Looking Back
- Knowing that, to draw a Sierpinski triangle, each existing triangle has to draw three smaller Sierpinski triangles inside of it, can you explain in your own words why the runtime is relatively flat early on yet increases sharply at higher levels?
- How much does moving from level 13 to 14 improve the look of the fractal versus moving from level 3 to 4? How much do their respective runtimes change?
- Use the equation of your best-fit line to predict how long it would take for the program to complete 20 iterations.
- If you had a computer that was twice as fast, would you be able to draw 20 levels in a reasonable time? How many times faster would your computer have to be to draw 20 iterations in 10 seconds?

