Readers familiar with the physics of open quantum systems have probably encountered a functional parametrization (ohmic, super-ohmic, etc.) for a thermal bath of linearly coupled, non-interacting harmonic oscillators. Physically motivating these models from the atomistic structure of a quantum material is a difficult and expensive semi-classical process, but the detailed structure of the bath can drastically alter short time population dynamics. The most satisfying procedure I am aware of consists of:

1) Performing a closed-dynamics (usually classical) simulation of quantum system and environment, somehow partitioning system and environment so you can monitor energy fluctuations of the system.

2) Taking the resulting energy fluctuation time-series constructing the real, symmetric classical correlation function.

3) Semi-classically extending this correlation function to obey the quantum conditions for causality and detailed balance while performing a Fourier transform to obtain the frequency dependent model for the harmonic bath.

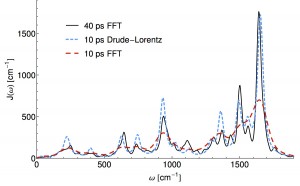
In terms of wall-time, step 1) is most expensive because something like ab-initio MD needs to be run for a length time going as the inverse frequency of the slowest bath mode (40ps or so) while sampling the quantum Hamiltonian in the classical environment. In this recent work Thomas Markovitch reduced by a factor of roughly 8 the required MD simulation time, by exploiting a sparse l1 signal processing technique (super-resolution). As an added bonus the l1 technique decomposes the spectral density into an analytical form which yields an analytic non-Markovian bath kernel. This is a step towards “black-box” baths which are more than three parameters of an Ohmic function. (ArXiv)

Personal hero and noted banjo enthusiast Bill Miller often poses the following thought experiment to critique classical MD:

The zero point energy in the ~3000 wavenumber modes of water is more than 20 times larger than Kb*T at room temperature. If you gave these degrees of freedom their ZPE in classical MD that ZPE would leak into other modes, at the very least resulting in a high effective temperature.

In protein simulations this isn’t an immediate problem because high-frequency oscillators are frozen out by the SHAKE algorithm (to allow for large integrator timesteps) and given no zero point energy. Clearly it would be nicer to treat the quantum effects in the MD. People in this field know there are many, many ways to do this, usually based on some scheme to approximately integrate the path integral, but nothing as simple as running CHARMM or CPMD.

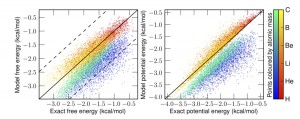
In this pre-print Ryan Alan and I propose an alternative: generate an effective force field which reproduces the density of the quantum system under the laws of classical statistical mechanics. We show such a potential exists, and that the map between the physical potential and the fictitious effective potential is unique. You can think of this like DFT for quantum MD, it takes a simulation which is easy to perform (classical MD/MC) and gives you the exact density. The catch is that you need to come up with this mapping that contains all the information about the difference between the quantum and classical effective potentials. (something like the problem of knowing the exact functional). We also numerically inverted that map for some low dimensional systems.

In the time between finishing my post-doc and beginning the group I’ve been indulging my appetite for random quantum ideas outside of the electronic structure realm. Jarrod McClean came up with this pretty wild adaptation of quantum computing’s ancilla concept to do quantum dynamics. The approach (which we cast as a version of the quantum time-dependent variational principle) has some interesting features, and we eventually managed to do parallel in time dynamics with it. (arXiv)