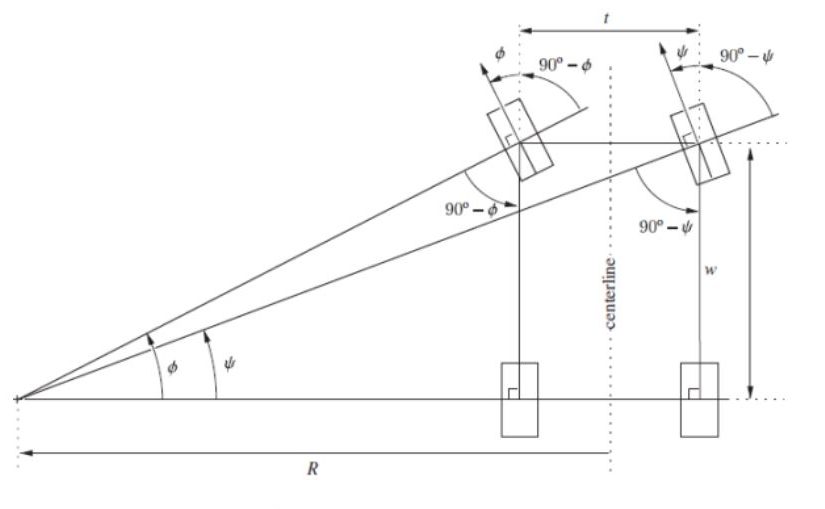
As part of AME 40423 – Mechanisms and Machines, design project asked for synthesis of a four bar steering mechanism for a car such that it followed an Ackerman function, which describes the the angle of each of a car’s two front wheels such that the car can turn without slipping about any radius turn. In order to allow for symmetric turning, the mechanism was required to be symmetric. Additionally, the grounded link of the mechanism had a set length, as it was constrained by the track of the car.
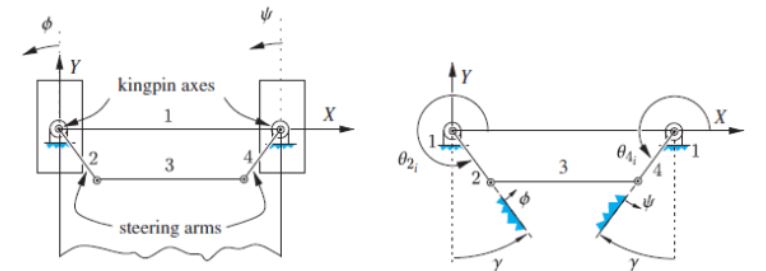
In order to synthesize the mechanism, Fruedenstein’s equation was used with both a 3 point point-matching method and a single-order derivative-matching method. Both resulting functions were compared against the desired function for set conditions in order to demonstrate proper execution of both methods. The results can be seen in the below figure.
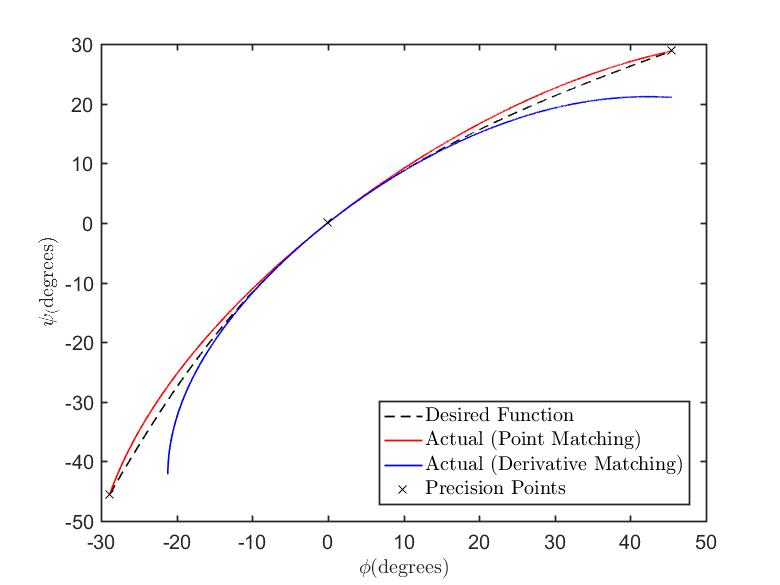
After this optimization of the system was left up to the student as an exercise.
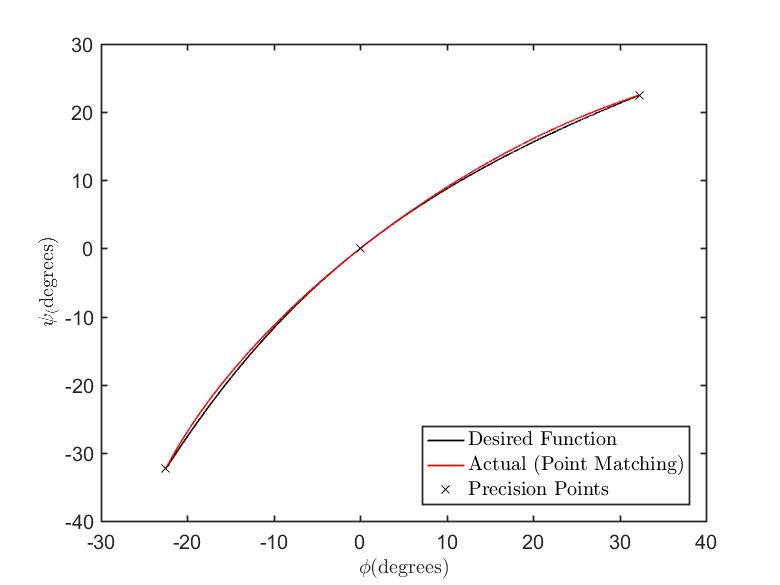
I chose to try to optimize the system using the point-matching method. First I tried to match the points for a more reasonable turn radius, as the originally desired turn radius resulted in a fair amount of error. The wheelbase of the car was given to be 5 feet, while the originally requested turn radius was given to be 7 feet. In order to decreased error, a turn radius of 10 feet was chose for the precision points. This resulted in a mechanism which produced the function displayed in the below figure.
I then chose to further investigate the relationship between increasing the precision point turn radius and the error of the resulting function. Thus I synthesized the mechanism for various precision point turn radii, and plotted the resulting normalized error as a function of the number of feet it was increased from the original turn radius of 7 feet. The resulting plot is displayed below.
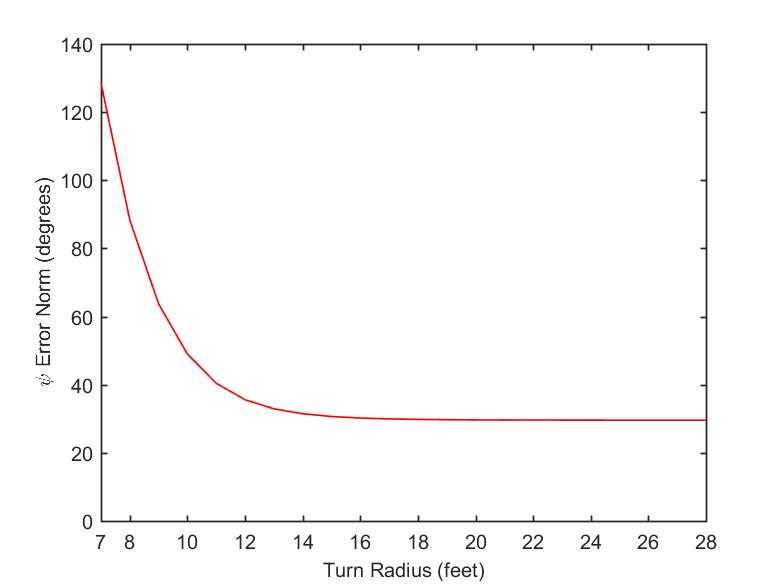
Interestingly, the normalized error decreases significantly until the turn radius is greater than 10 feet (twice the wheel base), when it starts to decrease at lower rates until it seems to reach an asymptote.