Our group works on problems where we can make a contribution to both computational mathematics and cell biology.
As the quantitative biologist Wallace Marshall once asked me: “What’s in it for the mathematicians?”
With this in mind, our research has a dual-track focus. In biology, we are using modeling and simulation to understand self-organization in the actin cytoskeleton. On the mathematical side, we are developing new numerical methods to simulate cytoskeletal mechanics and biochemistry. See the links at left for specific projects.
What biology are we studying?
Composed of actin filaments, cross linkers, and myosin motors, the actin cytoskeleton generates and sustains mechanical forces capable of dividing, polarizing, and moving the cell, thus shaping embryonic development, cancer cell metastasis, and wound healing. Regulation of the cytoskeleton is often viewed in a “linear” manner, where steps in a signaling cascade yield a network with the organization necessary for the task at hand. Recent evidence, however, has demonstrated that cytoskeletal organization actually emerges from a complex microscopic interplay between actin assembly, myosin-induced contractility, and activator-inhibitor coupling of actin with its regulators. A fundamental question is how the cell manipulates these molecular-scale interactions to turn the cytoskeleton into a semi-autonomous machine, able to sense and correct mistakes, adapt to new surroundings, and process information from its environment.
The primary component of the cytoskeleton is actin filaments, inextensible fluctuating fibers which organize into linear and branched architectures. The images below show simulation actin filaments, in vitro branched structures, and in vivo architectures in the C. elegans embryo.
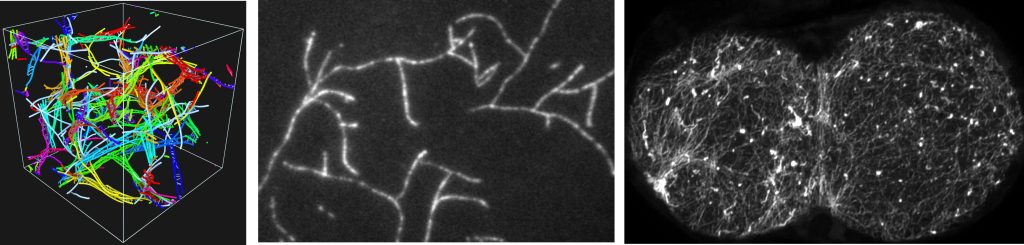
We are working with experimentalists in the Munro, Kovar, and Bement labs to study how filaments self-organize on the cell scale through interactions on the molecular scale.
What “new math” are we developing?
Actin networks present challenges for numerical methods. Filaments are slender and inextensible, cross linkers are stiff, and dynamics occur in a suspending fluid which immerses the filaments and moves them around. Broadly speaking, our numerical methods focus on Brownian motion under constraints (see [1] linked below). Recently, we have become more interested in coupling these kinds of simulations to experimental data through an inverse problem framework. See project links at left for more information.
Representative publications
- Maxian O., Dinner A., and Munro E. (2025). Actin network heterogeneity tunes activator-inhibitor dynamics at the cell cortex. (Under review).
- Maxian, O., & Donev, A. (2024). A simulation platform for slender, semiflexible, and inextensible fibers with Brownian hydrodynamics and steric repulsion. Physics of Fluids, 36(12).
- Maxian, O., Peláez, R. P., Mogilner, A., & Donev, A. (2021). Simulations of dynamically cross-linked actin networks: morphology, rheology, and hydrodynamic interactions. PLoS computational biology, 17(12), e1009240