I made the following question for the final exam of my “Philosophical Issues in AI” class:
Your dad asks you: why LLMs can generate eloquent essays, but sometimes make mistakes in very basic arithmetic? Give an accessible explanation to him based on your knowledge of how LLMs are built. You might want to mention the distinction between logicist AI and machine learning based AI.
Here’s an answer generated by ChatGPT (free version running GPT4o):
Large language models (LLMs) like ChatGPT are built using machine learning, not traditional logic-based AI. They don’t “think” like humans or perform step-by-step calculations like a calculator. Instead, they generate text by predicting the most likely sequence of words based on patterns they’ve learned from massive amounts of data.
When writing essays, this predictive approach works well because language is full of patterns—grammar, style, and logical flow—that LLMs can model effectively. They’ve been trained on vast amounts of well-written text, so they can mimic fluent and persuasive writing.
However, arithmetic requires precise rule-based reasoning, which LLMs struggle with. Unlike a logicist AI, which follows explicit rules to compute correct answers, LLMs rely on statistical correlations. While they may have seen many examples of simple arithmetic in their training data, they don’t “understand” numbers in a mathematical sense. Instead of performing calculations, they generate an answer that seems statistically likely, which can lead to errors, especially with less common problems.
Some modern AI systems try to bridge this gap by integrating symbolic reasoning (logic-based methods) with machine learning, but LLMs alone remain better at natural language than strict computation.
As far as the exam goes, this is an OK answer, and it will likely satisfy your dad as well. However, if we are interested in the specific question of the outlook of language models doing mathematics (as I am), then the analysis based on a dichotomy between statistics vs. rule-following appears way too generic.
The statistics vs. rule-following distinction has been there since the very beginning of AI, and there were long debates on whether neural networks can learn rules. Some people thought that the ability to follow grammatical rules is a fundamental aspect of natural language competence. Then it seems natural to suspect that neural networks are inherently limited in learning language — just replace the word “arithmetic” with “linguistic” in the third paragraph written by ChatGPT. Arguments like this are based on the following premises:
- Ability \(X\) is rule-based.
- If \(X\) is rule-based, then neural networks/transformers/LMs are inherently limited in learning \(X\).
However, contemporary LMs appears to significantly challenge, if not falsify, these two premises when \(X\) = natural language competence. Once we accept that these LMs are fairly linguistically competent, then we must accept that either natural language is not based on rule-following, or neural networks can learn the relevant rules (the “either … or” is not exclusive). It seems to me that when \(X\) = natural language competence, neither of the two premises is quite convincing. In contrast, the version of the argument with \(X\) = arithmetic/mathematics remains somewhat consistent with our observation of current LMs. It might be falsified in a few years, in a way similar to the argument on language. Or it may have some merit in that arithmetic/mathematics is indeed based on some rules that are difficult for LMs to learn. Still more, it might be that arithmetic/mathematics remains difficult for LMs, but for reasons that have nothing to do with rule-following. The goal of this post is to give some analysis on these thoughts.
The idea of rule-following has interested philosophers, who have identified some weird phenomena related to it:
- (Lewis Carroll) A rule is not reducible to a bunch of statements. One can accept many statements that state a rule, without actually following the rule.
- (Wittgenstein) Given finitely many instances of a rule, we cannot uniquely identify this rule, which makes it difficult to communicate your intended rule. E.g. you can ask a kid to complete the sequence \(1, 3, 5, 7, ?\) and the kid replies \(111\), because she is following the rule “write all the roots of \((x-1)(x-3)(x-5)(x-7)(x-111)=0\)”, not your intended rule of “write the next odd number”.
- (Kripke) These observations leave room for a kind of radical skepticism: throughout human history we have performed finitely many instances of addition. How do we know that we were actually following the rule of addition, not some weird operation that happens to be consistent with addition at the instances that we have already performed?
The upshot is that based on empirical evidence, it is theoretically difficult to tell whether someone is following rule \(X\), rule \(Y\), rule \(Z\), or not following any rules at all. However, as in a lot of skeptical scenarios, there is a “say-no-to-over-philosophize” response here, analogous to Moore’s “proof” of external world, or Hume’s “solution” to the problem of induction. In reality, we make a lot of efforts to make sure someone/something is following a specific rule (or behaves as if it is following this rule):
- We give kids exams to make sure that they learn the rule and algorithm for addition.
- We give chips a lot of tests to make sure that they are following the rules that they are designed to follow.
- ……
While these activities do not really address philosophical skepticism, they are able to give us an operational guarantee (as opposed to a theoretical/philosophical guarantee) of rule-following-like-behavior, which seems to be all we want in practice. From the practical point of view, what matters is: how should we characterize this operational bar? Have LMs already passed this operational bar? If not, will they?
The most straightforward operational bar is scoring high in exams. For example, here’s how some leading LMs do in multiplying two numbers:
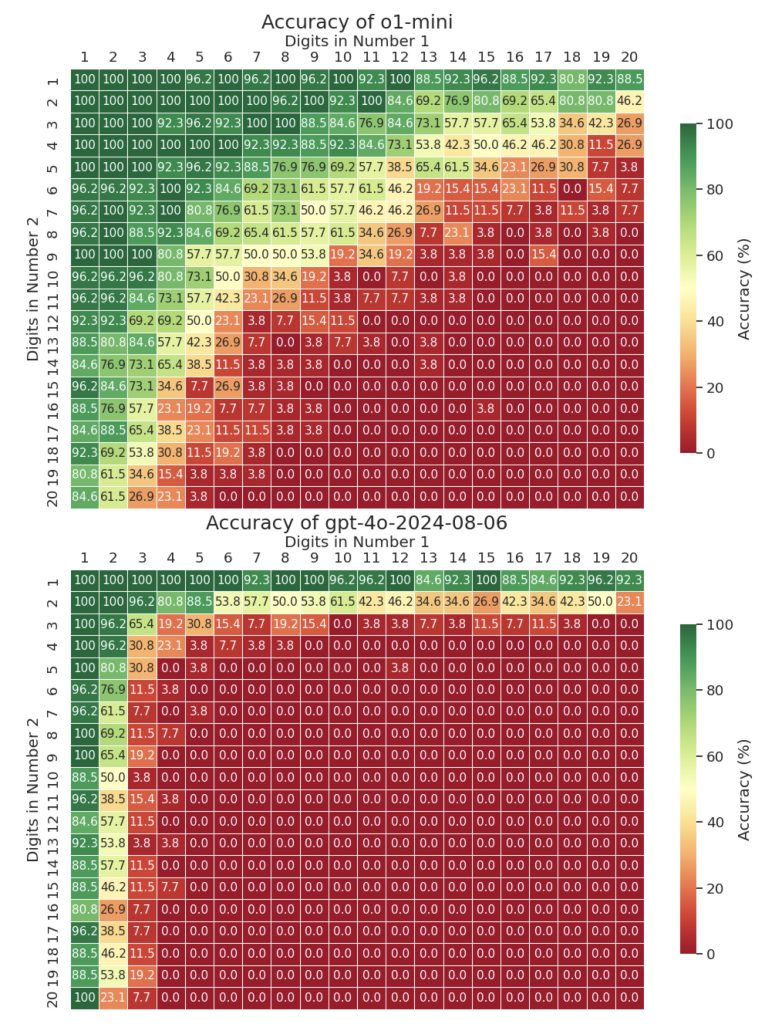
How should we interpret outcomes like this? It seems hard to say that o1-mini knows how to do multiplication if it scores merely 69.2% in multiplying 6-digit numbers by 8-digit numbers. On the other hand, when we give 9-year-olds multiplication exams, wo don’t ask them to multiply 6-digits by 8-digits. A kid would pass if she can do 4-digits by 4-digits perfectly (which o1-mini also can). Does this result give any guarantee that she will be more accurate than o1-mini when doing \(m\)-digits by \(n\)-digits? Furthermore, I suspect that when \(m, n\) is large, humans are surely prone to errors. Even if they can do it, it will take a long time and most people will quickly lose patience without seeing it as any meaningful indication of their command of multiplication.
Perhaps test score is too naive to be an operational bar for rule-following. Perhaps the commandment of a rule is signified not by the correctness of the answer, but by some property of the process leading to the answer, and that is why we want the kid to “show-the-work” (analogous to “Chain-of-Thought” (CoT) for LMs). If the kid demonstrates that she is applying the right algorithm, we conclude that she has a good understanding, even if her process may contain a few errors. Once we are convinced that she has mastered the algorithm, which is in principle applicable to multiplying \(m\)-digits by \(n\)-digits for any given \(m\), \(n\), we conclude that she learned multiplication. Can we apply this method to LMs? It seems there are major challenges, both empirically and theoretically.
One may try to use CoT to address this problem, by using CoT prompts or incorporating more sophisticated CoT methods such as “reasoning models”, which significantly improves test scores in practice. But it seems to me that this may not suffice for our purpose — examining rule mastery by inspecting the process leading to the LM’s answer. The idea that CoT works for this purpose depends on the assumption that CoT indeed showcases the internal workings of the LM leading to the answer — a questionable assumption as CoT is essentially more output from the LM! (Compare this situation with show-the-work, which strikes me as something that actually shows how a human arrive at an answer.) When a “reasoning model” makes an error in its CoT and one tries to correct it, the situation is strikingly similar to Achilles talking to the Tortoise as in Lewis Carroll — the Tortoise keeps repeating correct statements of an inference, and yet refuses to actually make that inference.
Is there a way to actually probe the internal workings of the LM? I learned that a subject in AI research called “mechanistic interpretability” seeks to address this question. The idea is that by inspecting and experimenting with a post-training neural network, we can identify the functional roles of its various components, and give high-level descriptions of how it completes certain tasks. One prominent example is the discovery that relatively simple networks learn modular addition by converging to some identifiable algorithm, and in fact similar architectures can learn multiple different identifiable algorithms to do it (see the paper https://arxiv.org/abs/2306.17844 which appears quite interesting). However, it seems to me that current mechanistic interpretability research is limited to relatively simple toy networks and problems, and the complex networks in real usage are hardly mechanistically interpretable.
On the other hand, approaching the question of rule-following from a theoretical point of view appears difficult as well. After all, the LM is following a complex rule — it converts your input into a vector, multiplies it by some huge matrices for many times, and eventually gives you an output (modulo some pseudorandomness). Rule-following-like-behavior takes place when given certain inputs, this complex rule reduces to some simple rules. The question is to theoretically study when and why this phenomenon takes place, which appears to be highly difficult and intangible at the current state of knowledge. Part of the difficulty lies in the fact that a trained neural network involves multiple aspects: the architecture, the training data, and the training method, with the latter two highly empirical in nature. Consequently, a mere mathematical analysis of the architecture is unlikely to help.
If these obstacles can be partly overcome, e.g. if we have an explanation of why GPT4 is able to generate programs that actually work via some mechanistic analysis, I imagine this will satisfy the LM-rule-learning skeptics to a large extent. In fact, I think part of the frustration that drives their argument comes from the sentiment that lacking such analysis, any empirical success of LMs appears like some miracle. In response to these sentiments, LM proponents often appeal to unhelpful general concepts such as “grokking”, “scaling”, “emergence”, or to the recorded successes in the past few years, which are unconvincing responses. Consequently, LM errors are more likely to be interpreted as evidence of lack of understanding, instead of sympathetically interpreted as unintended errors. With more mechanistic understanding of LMs, the situation may be reversed.
To summarize, we arrive at the following conclusions:
- From a radical philosophical point of view, it is difficult in general to empirically determine whether something follows rules, regardless whether it is human or LM.
- From a practical point of view, mere exam score appears to be a poor indication of rule-following.
- However, mechanistic analysis may be applicable to both humans and LMs as indications that they are following rules.
- Mechanistic analyses of LMs are technically difficult, so there is no definitive proof that LMs can/cannot follow rules.
- Maybe there are alternative empirical verifications of rule-following such that humans can be easily verified and LMs cannot, but I am not aware of any. (The idea of ARC-AGI is similar to this, however it is still based on mere exam scores for a set of more diverse and creative rules, and lacks a mechanistic component/alternative method of empirical verification.)
- Absent these analyses, it seems premature to assert that LMs intrinsically cannot learn certain rules.
So far our discussion is limited to the case of arithmetic, and we are ultimately interested in the outlook of AI doing more advanced (by human standard) mathematics. Researchers have created a number of math benchmarks for AI to this end, and two of them are of particular interest: FrontierMath and PutnamBench. In a later post, I shall discuss some observations on these benchmarks and related topics.
