This article investigates whether an algorithm can provide an undiscovered physical phenomenon by detecting patterns in the region where the data collected. The pattern recognition is considered with the basis of inferential statistics, which differs from descriptive statistics, as McAllister implied. I assert that physical patterns should be correlated with mathematical expressions, which are interconnected with the physical (quantitative) laws. The known unknows, e.g. gravitons, and the unknown unknowns, e.g. fifth force of the universe, are examined in the sense of learning capabilities of an algorithm based on empirical data. I claim there is no obstacle preventing algorithms from discovering new phenomena.
Nazli Turan*
*Department of Aerospace and Mechanical Engineering, University of Notre Dame
1.Introduction. The notion of discovery has occupied many philosophers’ mind in a variety of angles. Some tried to formulate a way through a discovery, although some desperately tried to fix the meaning (e.g. the eureka moment) without considering the time as a variable. Larry Laudan pointed out two motives yielding a discovery: pragmatic aspect, which is a search for scientific advancement, innovation or invention; epistemological aspect, aiming to provide well-grounded, sound theories. He made a clear distinction between discovery and justification, attaining the latter as an epistemological problem. Although I’m aware of this distinction, I tend to accept that those are intermingled, even in his example: “Self-corrective logics of discovery involve the application of an algorithm to a complex conjunction which consists of a predecessor theory and a relevant observation. The algorithm is designed to produce a new theory which is truer than the old. Such logics were thought to be analogous to various self-corrective methods of approximation in mathematics, where an initial posit or hypothesis was successively modified so as to produce revised posits which were demonstrably closer to the true value.” (Laudan, 1980). In my understanding, every pre and post processes are a part of justification, while the outcome of an algorithm is a discovery. I will pursue his analogy of self-corrective logics and transform into literal computer algorithms to examine whether a computer algorithm (or artificial intelligence, AI, machine learning program, deep neural network) can reveal undiscovered phenomena of nature.
To decide on whether the algorithm implies a true description of the real world, I rely on the empirical adequacy principle proposed by Van Fraassen. The collected, non-clustered empirical data is the input to an algorithm which is capable of unsupervised learning to avoid user’s biases. The data and resulting conclusions will be domain-specific, meaning; the algorithms, which can only interpolate the relations and patterns buried in the data, are the main concern of this paper, although there are preliminary results for physics-informed neural networks, which have extrapolation capabilities that are not within the train data (Yang, 2019).
In my view, the algorithms of interest are scientific models acting on the structured phenomena (consisting of set of patterns and relations) and utilizing mathematical expressions accompanied with statistical nature of data. The inferential statistics (in Woodward’s sense) is emphasized after making a clear distinction between the systematic uncertainties (due to resolution or calibration of the instruments) and the precision uncertainties (due to sampling of data). McAllister’s opposition to Woodward and his concerns about patterns in empirical data are elaborated in the second section and the examples of probabilistic programming which includes an application of inferential statistics are investigated. The third section will be a discussion of learning and interpolating capabilities of algorithms. Lastly, I will point out the known unknowns (gravitons) and the unknown unknowns (the fifth force) in the scope of conservation laws to discuss the possibility of discovery by computer algorithms.
2. Physical structures have distinguished patterns. Before considering the capabilities of an algorithm, I want to dig into the relation between empirical data and physical structures. There are two questions appearing immediately. First: is the world really a patterned structure? Second: are we able to capture patterns of the physical world analyzing empirical data? These questions have broad background, but I would like to emphasize some important ones here. Specifically, the latter question is my point of interest.
Bogen and Woodward shared their ideas in an atmosphere where the unobservables are still questionable (Bogen, Woodward 1988). They eagerly distinguished data from phenomena, by stating that ‘data, which play the role of evidence for the existence of phenomena, for the most part can be straightforwardly observed. (…) Phenomena are detected through the use of data, but in most cases are not observable in any interesting sense of that term.’ Bogen explains further his views on phenomena: “What we call phenomena are processes, causal factors, effects, facts, regularities and other pieces of ontological furniture to be found in nature and in the laboratory.” (Bogen, 2011). I will assert parallel claims to their statements with some additions. The recorded and collected data is the representation of regularities in phenomena. These regularities may provide a way to identify causes and effects. Apart from these, we are in an era where we’ve come to realize that directly unobservable objects might be real, such as Higgs boson and gravitational waves. Our advancements in building high-precision detectors and in understanding of fundamental interactions paved the way for scientific forward steps. I believe the discussion of observable vs. unobservable objects is not relevant anymore. Therefore, I’m inclined to accept that data provides strong evidence of phenomena whether they are observable or not. Yet, the obtained data should be regulated, clustered, and analyzed by mathematical and statistical tools. Bogen and Woodward was ending their discussion by illuminating both optimistic and pessimistic sides of the way starting from data to phenomena:
“It is overly optimistic, and biologically unrealistic, to think that our senses and instruments are so finely attuned to nature that they must be capable of registering in a relatively transparent and noiseless way all phenomena of scientific interest, without any further need for complex techniques of experimental design and data-analysis. It is unduly pessimistic to think we cannot reliably establish the existence of entities which we cannot perceive. In order to understand what science can achieve, it is necessary to reverse the traditional, empiricist placement of trust and of doubt.” (Bogen, Woodward 1988)
Inevitably, some philosophers started another discussion of patterns in empirical data, by questioning how to demarcate patterns that are physically significant. James W. McAllister supposed that a pattern is physically significant if it corresponds to a structure in the world, but then he thought all patterns must be regarded as physically significant (McAllister, 2010). I agree with the idea that physical patterns should differ from other patterns. Physical patterns should be correlated with mathematical expressions which are interconnected with the physical laws. Opposing the McAllister’s idea that all patterns are physically significant, I can give an example of Escher’s patterns, which are artistically designed by the Dutch graphic artist M.C. Escher. If we take the color codes or pixels of his paintings as empirical data, sure we can come up with a mathematical expression or pattern to produce his paintings, but that pattern does not correspond to a physical structure. To support my claim, I can provide another example of parameterization to express the designs Escher created. Craig S. Kaplan from Computer Graphics Lab at University of Waterloo approached to the problem with a unique question: Can we automate the discovery of grids by recognizable motifs? His team developed an algorithm that can produce Escher’s patterns (see Fig.1 adapted from the website: Escherization).

If we are convinced that Escher’s patterns are not corresponding to any physical structure in the world, I would like to discuss the physical patterns in data with noise or error terms. I don’t use ‘noise’, because this term is used mostly in signal processing, so it has some limitations in the connotation. Besides, for the people outside the scientific research, ‘noise’ would be conceived as unwanted or irrelevant measurements. ‘Error’ is frequently used in data analysis, but again I prefer to avoid misunderstandings about its physical causes. I will continue with ‘uncertainty analysis’ of the measured data. There are two types of uncertainties in data: systematic uncertainties, which stem from the instrument calibration and resolution, and precision uncertainties, which are due to the repetitive sampling of the system (Dunn, 2010). To analyze these uncertainties, we assume that they have a random (normal/Gaussian) distribution. I want to give an example from my specific area of research: the lifetime of the current peaks (Fig.2). Here in the figure, there are three current peaks and I want to estimate their duration (time in x-axis) by descriptive statistics. I decide to be in a 95% confidence level assuming the normal distribution of current peaks. 12 ns, 14 ns, and 20 ns are measured respectively. I can easily find their mean and the standard deviation of the mean (up), 15.33± 4.16 ns. However, this is not correct. In the figure, you can see step-by-step increments of the current, which is due to the time resolution of the oscilloscope, 2 ns. I need to consider this systematic uncertainty (us) .

Up to this point, I mostly made some mathematical manipulations to represent data in a compact way. One important assumption was the normal distribution of uncertainties which is observed frequently in nature, for example in human height, blood pressure etc. The other key attempt was to choose a confidence level. Now, it is time to discuss inferential statistics. What type of information I can deduce form empirically measured data? For example, here I observed that the lifetime of the current peaks is increasing from the first one (12 ns) to the third one (20 ns). Is there any physical reason causing this? Can I conduct analysis of variance or can I test my hypothesis that if I run the current for longer time, I will observe longer lifetimes (>20 ns)? Even though scientists would choose to use descriptive statistics largely to show their data in graphs or tables, they are -in general- aware of the causes behind the empirical data yielding some trends or patterns. These patterns are the footprints of the physical structures, in other words, phenomena.
In McAllister’s paper (2010), the term ‘noise’ is used so arbitrarily that he thought noises can add up, although we cannot add them up if the parameters are dependent on each other. He provided an example for the deviations in the length of a day (Dickey 1995). His argument was the noise is not randomly distributed and it has a component increasing linearly per century (1-2 µs per century). All the forces affecting the length of a day are illustrated in Dickey’s paper (Fig.3).

Dickey described all these individual effects as the following:
“The principle of conservation of angular momentum requires that changes in the Earth’s rotation must be manifestations of (a) torques acting on the solid Earth and (b) changes in the mass distribution within the solid Earth, which alters its inertia tensor. (…) Changes in the inertia tensor of the solid Earth are caused not only by interfacial stresses and the gravitational attraction associated with astronomical objects and mass redistributions in the fluid regions of the Earth but also by processes that redistribute the material of the solid Earth, such as earthquakes, postglacial rebound, mantle convection, and movement of tectonic plates. Earth rotation provides a unique and truly global measure of natural and man-made changes in the atmosphere, oceans, and interior of the Earth. “(Dickey, 1995, pg.17)
It is beautiful that a group of researchers spent quite a time to upgrade their measurement tools and the author explains how they tried to reduce the systematic uncertainties by upgrading their tools (pg.21 in the original article). And, the entire paper is about hourly/monthly/yearly patterns affecting the length of a day and how their measurement tools (interferometers) are capable of detecting small changes. Dickey clearly states that ‘an analysis of twenty-five years of lunar laser ranging data provides a modern determination of the secular acceleration of the moon of -25.9 ± 0.5 arcsec/century2 (Dickey et al.,1994a) which is in agreement with satellite laser ranging results.’ He provided the noise term for this specific measurement and there is no clue to assume it is not randomly distributed, as McAllister claimed. Dickey captured the oscillations (patterns) changing in a time-scale of centuries in the data and supported his empirical data by physical explanations; tidal dissipation, occurring both in the atmosphere and the oceans, is the dominant source of variability. After all, one important aspect I wanted to state against McAllister’s account of describing patterns is that the empirical data can yield a causal relation which can be understood as pattern, besides the uncertainties in the sense of inferential statistics might provide information about patterns too.
Inferential statistics entails with a probabilistic approach, in general. One application for computer algorithms is Bayesian probabilistic programming which adopts hypotheses that make probabilistic predictions, such as “this pneumonia patient has a 98% chance of complete recovery” (Patricia J Riddle’s lecture notes). With this approach, algorithms combine probabilistic models with inferential statistics. MIT Probabilistic Computing Project is one of the important research laboratories in this area. They offer probabilistic search in large data, AI assessment of data quality, virtual experiments, and AI-assisted inferential statistics, “what genetic markers, if any, predict increased risk of suicide given a PTSD diagnosis and how confident can we be in the amount of increase, given uncertainty due to statistical sampling and the large number of possible alternative explanations?” (BayesDB). The models that they use in BayesDB are ‘empirical’, so they expect them to be able to interpolate physical laws in regimes of observed data, but they cannot extrapolate the relationship to new regimes where no data has been observed. They showed the data obtained from satellites interpolated to Kepler Law (Saad & Mansinghka, 2016).
3. Empirical data can be interpolated to physical laws. The empirical data sets can be used as raw input to an algorithm which can be trained to distribute data in subsections. If this algorithm can yield relations between data sets, we might be able to obtain physical laws in regimes of observed data. There are two main concerns here: the possibility to impose user’s biases in parametrization and the user’s capability to understand the pointed result. The first obstacle has been overcome by unsupervised learning programs. The latter needs to be elaborated.
Algorithms (both recursive and iterative ones) have black boxes, which promotes an accessibility problem to mid-layers of algorithms. Emily Sullivan states ‘modelers do not fully know how the model determines the output’ (Sullivan, 2019). She continues:
“(…) if a black box computes factorials and we know nothing about what factorials are, then our understanding is quite limited. However, if we already know what factorials are, then this highest-level black box, for factorials, turns into a simple implementation black box that is compatible with understanding. This suggests that the level of the black box, which is coupled with our background knowledge of the model and the phenomenon the model bears on (…)” (Sullivan, 2019)
She has a point to state the relation between black boxes and our understanding; however, this relation does not override the possibility of discoveries. The existence of black boxes is not a limitation for an algorithm which may yield unknown physical relations. The limitation is our understanding. As once Lynch named his book, Knowing More and Understanding Less in the Age of Big Data, we’re struggling in between knowing and understanding. On the other hand, algorithms are acting on the side of ‘learning’. Although the concept of learning is worth to be discussed philosophically, I will consider it in the sense of computer (algorithm) learning. There are seven categories of algorithm learning: learning by direct implanting, learning from instruction, learning by analogy, learning from observation and discovery, learning through skill refinement, learning through artificial neural networks, learning through examples (Kandel, Langholz 1992). For the case of learning from observation and discovery, the unsupervised learner reviews the prominent properties of its environment to construct rules about what it observes. GLAUBER and BACON are two examples investigated in elsewhere (Langley, 1987). These programs bring in ‘non-trivial discoveries in the sense of descriptive generalizations’ and their capabilities to generate novelties have been questioned (Ratti, 2019). The novelties might be subtle, but they are still carrying the properties of being a novelty which was hidden to human knowledge before.
I realized that people tend to separate qualitative laws and quantitative laws, implying that algorithms are not effective for the laws of qualitative structures because human integration is necessary to evaluate novelties (Ratti, 2019). I want to redefine those by drawing the inspiration from Patricia J Riddle’s class notes on ‘Discovering Qualitative and Quantitative Laws’ such that, qualitative descriptions state generalizations about classes, whereas quantitative laws express a numeric relationship, typically stated as an equation and refer to a physical regularity. I’m hesitant to call qualitative descriptions as laws because I believe this confusion stems from the historical advancement of biology and chemistry. Here, I want to refer to Svante Arrhenius (Ph.D., M.D., LL.D., F.R.S. Nobel Laureate Director of The Nobel Institute of Physical Chemistry, pretty impressive title!) who wrote a book ‘Quantitative Laws in Biological Chemistry’ in 1915. In the first chapter of his book, he emphasized the historical methods of chemistry:
“As long as only qualitative methods are used in a branch of science, this cannot rise to a higher stage than the descriptive one. Our knowledge is then very limited, although it may be very useful. This was the position of Chemistry in the alchemistic and phlogistic time before Dalton had introduced and Berzelius carried through the atomic theory, according to which the quantitative composition of chemical compounds might be determined, and before Lavoisier had proved the quantitative constancy of mass. It must be confessed that no real chemical science in the modern sense of the word existed before quantitative measurements were introduced. Chemistry at that time consisted of a large number of descriptions of known substances and their use in the daily life, their occurrence and their preparation in accordance with the most reliable receipts, given by the foremost masters of the hermetic {i.e. occult) art.” (Arrhenius, 1915)
The point I want to make is that our limited knowledge might require qualitative approaches, for example, in biology; however, the descriptive processes can only be an important part of tagging clusters while the mathematical expressions derived from the empirical data show the quantitative laws of nature. Furthermore, our knowledge and the presence of black boxes are not obstacles for unsupervised learning algorithms which can nicely cluster and tag data sets and demonstrate relations between them. As an example, a group of researchers showed that their algorithm can ‘discover physical concepts from experimental data without being provided with additional prior knowledge’. The algorithm (SciNet) discovers the heliocentric model of the solar system — that is, it encodes the data into the angles of the two planets as seen from the Sun (Iten, Metger et.al. 2018). They explained the encoding and decoding processes by comparing human and machine learning (Fig.4).
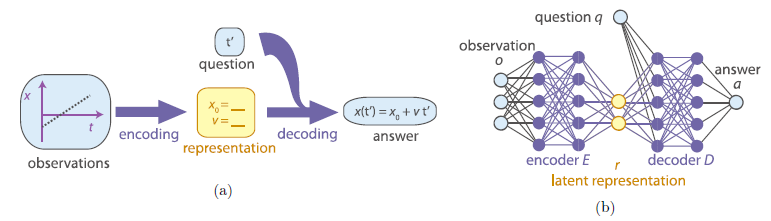
In human learning, we use representations (the initial position, velocity at a point etc.) not the original data. As mentioned in the paper, the process of producing the answer (by applying a physical model to the representation) is called decoding. The algorithm mentioned here produces latent representations by compressing empirical data. It utilizes probabilistic encoder and decoder during the process. As a result, researchers were able to recover physical variables from experimental data. SciNet learns to store the total angular momentum, a conserved quantity of the system to predict the heliocentric angles of Earth and Mars. It is clear that an unsupervised algorithm can capture physical laws (ie. conservation laws) through empirical data.
4. An algorithm can reveal unknown physical phenomena by analyzing patterns. Now, I want to explore the territory of unknown. Until now, I tried to show that physical structures have patterns which can be represented by mathematical expressions accompanied with inferential statistics. The expressions are correlated to the quantitative laws which govern the relations and interactions of phenomena. The observed empirical data includes a set of patterns and uncertainties. An unsupervised algorithm can take the empirical data and proceed descriptive tagging by itself. The layered process might be inaccessible to the user, but the black boxes do not prevent the discovery of physical laws. Therefore, an algorithm can interpolate the data in the observed region to physical laws. This process is a learning process for an algorithm although it is a little different than human learning.
As a curious human being, I wonder if algorithms would generate new physical structures that are unknown to today’s people. The first question is: why those structures are unknown? I can provide two primary reasons for this: either our instruments require some improvements to catch small changes buried in signal, or our understanding is limited to attain some meanings to observations. Gravitational waves were hypothetical entities until we upgraded our interferometers to capture the waves transmitted after the collision of two massive black holes. To tackle the limitations of our understanding is more challenging; however, history embodies many paradigm shifts such as the understanding of statistical thermodynamics, general relativity or wave-particle duality. If you would go to 15th century and tell the scientists of the time; the cause of static electric (electrons) follows uncertainty principle, so you cannot observe it when you measure it, the scientists would laugh at you so badly. Therefore, I never eliminate chances to find unknowns in science. This unknown can be a new particle, force, interaction, or process. Whatever the unknown is, I will assume it is a part of physical phenomena.
The second important question is: can we trust algorithms to find unknowns? First of all, the trained algorithms -supervised or unsupervised- have capability to learn, as I described in the previous section. To the best of my knowledge, such algorithms proved themselves to obtain Kepler laws, conservation laws and Newton laws (Saad & Mansinghka, 2016, Iten, Metger, et.al. 2018). That is to say, these algorithms are discovering the natural laws which were unknown to the 15th century humanity. I support that algorithms might provide the next generation physical laws or related phenomena and I don’t see any obstacle to prevent them to discover something new.
The third question would be: are those unknowns epistemically accessible to human understanding? Although this question is somewhat related to the first one, I want to explicitly state two possible unknowns: known unknowns and unknown unknowns. The first one would be claimed to exist but never detected before, such as gravitons, the carrier of gravitational force. The second one; however, would be never predicted to exist, such as the fifth force of nature. The most prominent challenge to detect a graviton is the impossible design of the detector which will weigh as much as the mass of Jupiter (Rothman & Boughn, 2006). The second problem is the nature itself; to detect a single graviton, we need to shield 1033 neutrino events and we do not have a monochromatic graviton source. That’s why graviton is accepted as a hypothetical particle. However, we cannot rule out its existence either. The latest LIGO interferometers collected data to prove the existence of gravitational waves, and some think this data can be used to predict the properties of gravitons (Dyson, 2014). Why don’t we feed our algorithms with these data? Maybe, they can provide the relations in deep data and eventually we can complete the puzzle of the standard model. The overarching goal to give this example is to emphasize the possibility of discovering unknowns. I must accept that empirical data might not guarantee to yield a solid result (i.e. the existence of gravitons); however, algorithm can point out the possibilities buried in data in a probabilistic way such as the probable mass of gravitons in certain limits.
Alternatively, algorithms might reveal unknown unknowns as a result. Before discussing this, I want to examine one of the latest findings in experimental physics: the fifth force. Physicist claim they’ve found a new force of nature (Krasznahorkay, 2019). The excited (energized) new particle decayed and emitted light which has been detected by a double-sided silicon strip detector (DSSD) array. The mass of the new force carrier particle is predicted by the conservation of energy. “Based on the law of conservation of energy, as the energy of the light producing the two particles increases, the angle between them should decrease. Statistically speaking, at least. (…) But if this strange boson isn’t just an illusion caused by some experimental blip, the fact it interacts with neutrons hints at a force that acts nothing like the traditional four.” (Mcrae, 2019).
The existence of a fifth force was totally unknown until the last month. Although it requires further evidences from other labs, no one was able to find misinterpretation of data, as far as I know. This does not mean that the finding is undeniable, but there is an anomaly regarding the law of conservation of energy. Previously, I showed some example algorithms yielding the conservation laws. My claim is that if an algorithm is able to capture the conservation laws, then it might reveal the relations of a new phenomenon, in this case, a new force! A force requires a carrier particle, which they termed the X17 particle with mass mXc2=16.70±0.35(stat) ±0.5(sys) MeV, where the statistical and systematic uncertainties are stated clearly (Krasznahorkay, 2019). My far-fetching point would be a humble suggestion for the researchers working on this type of projects where the detector data can be analyzed by algorithms to see if they can reveal a new relation.
5. Conclusion. The motivation to write this article was to ignite a spark about future possibilities of unsupervised learning algorithms. Although the capabilities of pattern recognition and generating novelties are questionable due to the qualitative aspect of the phenomena and the human factor involving while detecting new discoveries and understanding what the algorithm provides, I’m very optimistic about probabilistic programming construing with inferential statistics. Here, I showed the empirical data has distinguishable patterns than any other patterns (for example, artistic ones). The physical pattern can be represented by mathematical relations which are the traces of the physical phenomena. There are many algorithms capturing the physical relations based on the patterns in empirical data. They can also recover the physical laws of nature. Regarding all these points I made, I claim we would be able to discover new physical phenomena in the real word through algorithms. Apart from the incapable instrumental tools and our limited understanding, I don’t think there is a hurdle embedded inherently in a running algorithm. The unknowns are unknown to human being, not to the computer algorithms.
References
Laudan L. (1980). Why was the Logic of Discovery Abandoned?. In: Nickles T. (eds) Scientific Discovery, Logic, and Rationality. Boston Studies in the Philosophy of Science, vol 56. Springer, Dordrecht.
Van Fraassen, B. (1980). Arguments concerning scientific realism (pp. 1064-1087).
Yang, X. I. A., Zafar, S., Wang, J. X., & Xiao, H. (2019). Predictive large-eddy-simulation wall modeling via physics-informed neural networks. Physical Review Fluids, 4(3), 034602.
Woodward, J. (2010). Data, phenomena, signal, and noise. Philosophy of Science, 77(5), 792-803.
McAllister, J. W. (2010). The ontology of patterns in empirical data. Philosophy of Science, 77(5), 804-814.
Bogen, J., & Woodward, J. (1988). Saving the phenomena. The Philosophical Review, 97(3), 303-352.
Bogen, J. (2011). ‘Saving the phenomena’ and saving the phenomena. Synthese, 182(1), 7-22.
Kaplan, Craig S. (2000). Escherization http://www.cgl.uwaterloo.ca/csk/projects/escherization/
Dunn, P. (2010). Measurement and data analysis for engineering and science (2nd ed.). Boca Raton, FL: CRC Press/Taylor & Francis.
Dickey, J. O. (1995). Earth rotation variations from hours to centuries. Highlights of Astronomy, 10, 17-44.
Mansinghka, Vikash K. (2019). BayesDB. http://probcomp.csail.mit.edu/software/bayesdb/
Sullivan, E. (2019). Understanding from machine learning models. British Journal for the Philosophy of Science.
Lynch, M. P. (2016). The Internet of us: Knowing more and understanding less in the age of big data. WW Norton & Company.
Kandel, A., & Langholz, G. (1992). Hybrid architectures for intelligent systems. CRC press.
Langley, P., Simon, H. A., Bradshaw, G. L., & Zytkow, J. M. (1987). Scientific discovery: Computational explorations of the creative processes. MIT press.
Ratti, E, (2019). What kind of novelties can machine learning possibly generate? The case of genomics. (unpublished manuscript).
Riddle, Patricia J. (2017). Discovering Qualitative and Quantitative Laws. https://www.cs.auckland.ac.nz/courses/compsci760s2c/lectures/PatL/laws.pdf
Arrhenius, S. (1915). Quantitative laws in biological chemistry (Vol. 1915). G. Bell.
Iten, R., Metger, T., Wilming, H., Del Rio, L., & Renner, R. (2018). Discovering physical concepts with neural networks. arXiv preprint arXiv:1807.10300.
Saad, F., & Mansinghka, V. (2016). Probabilistic data analysis with probabilistic programming. arXiv preprint arXiv:1608.05347.
Rothman, T., & Boughn, S. (2006). Can gravitons be detected?. Foundations of Physics, 36(12), 1801-1825.
Dyson, F. (2014). Is a graviton detectable?. In XVIIth International Congress on Mathematical Physics (pp. 670-682).
Krasznahorkay, A. J., Csatlos, M., Csige, L., Gulyas, J., Koszta, M., Szihalmi, B., … & Krasznahorkay, A. (2019). New evidence supporting the existence of the hypothetic X17 particle. arXiv preprint arXiv:1910.10459.
Mcrae, M. (2019). Physicists Claim They’ve Found Even More Evidence of a New Force of Nature. https://www.sciencealert.com/physicists-claim-a-they-ve-found-even-more-evidence-of-a-new-force-of-nature/amp
