Cellular Automata

Difficulty: Beginner

Prerequisites

• This project has no prerequisites.

Background

Cellular automata is a fancy name for a grid of cells that changes based on a simple set of rules. The most famous example of a cellular automaton is Conway’s Game of Life. The rules of Conway’s Game of Life are as follows (copied from the Wikipedia article):

• Any live cell with fewer than two live neighbors dies, as if by underpopulation.
• Any live cell with two or three live neighbors lives on to the next generation.
• Any live cell with more than three live neighbors dies, as if by overpopulation.
• Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

By simply repeatedly applying these rules to a starting grid, you can create complex behavior like the “Gosper glider gun” below:

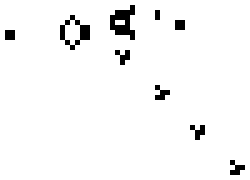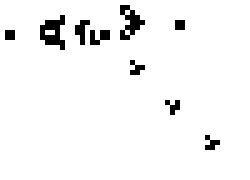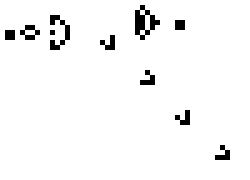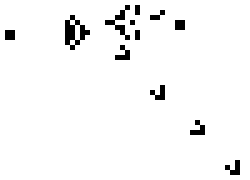
Cellular automata can create patterns that stay stable, repeat through a series of steps, move across the grid, or even spawn other patterns.

Mini-Game of Life

The King of Programmia wants as many things to be named after him as possible. So, he orders you to discover something interesting and name it after him. You decide to experiment with the Game of Life and name an interesting pattern after him, like the Gosper gun was named after Bill Gosper. After playing with the Game of Life for a bit, you have no idea how you are going to find something unique. Then, you come up with an idea.

Usually, the Game of Life is run on a large grid. In this project, you will look at the behavior of very small grids – those with dimensions smaller than 5×5. The tiny size of these grids lets you, with the help of a computer, go through every possible starting arrangement. This way, you can look for interesting behavior in a systematic way.

You will be provided with a Python script that plays the Game of Life on a grid size of your choosing. Since the edge cells don’t have as many direct neighbors as the center cells, the program considers the top edge adjacent to the bottom, and the left edge adjacent to the right. This keeps the rules consistent, with each cell having eight neighbors no matter its position. In the image below, the yellow cells are the eight neighbors of the red cell.

What to Do

1. Download life.py from here. Open the file for editing, read through it, and test it to get a basic understanding of how it works.
2. Find the section that begins with ### YOUR CODE GOES HERE ###. Any code put in that section will run for each possible starting configuration. There is already a simple example there for you to look at if you are confused.
3. The board is set to 3×3 by default, but you can change that in the code. Be warned that going much larger than 4×4 will make going through each possible combination take a long time, even for a computer.
4. While it’s up to you to decide exactly what you want to look for, it might be a good strategy to filter out the configurations that completely stop changing after a few steps. Then, go through the rest and note any interesting behavior.
5. Of the unique configurations you found, try to classify them. Graph how many configurations survive (keep changing) after 1, 2, 3… steps.
6. Once you have analyzed 3×3 boards, try a variety of different dimensions. Try to come up with explanations for the different behavior you see.

Looking Back

• How does the aspect ratio (thinness vs. squareness) of small boards affect the behavior of the Game of Life?
• How and why does the Game of Life operate differently on small boards than really big ones?
• What are the shapes of your “survival” graphs? How does the shape of the graph change when you change the dimensions of the board? Why might this be?
• Why would this method of exploration not work for, say, a 20×20 board? What approach might you take to analyze larger boards?