Titles and Abstracts

Notre Dame PDE Workshop, Department of Mathematics, May 3-5, 2024

---

Progress Report on Instability and Non-uniqueness
Dallas Albritton, University of Wisconsin-Madison

I will present forthcoming work with Giulia Mescolini and Maria Colombo (EPFL) in which we
investigate the (non-)existence of a selection principle for the 2D Euler
equations near Vishik’s self-similar vortex.

---

Concerning Gevrey Class Estimates for a Fluid-Structure Interactive PDE System
George Avalos, University of Nebraska-Lincoln

In this talk, we discuss higher regularity properties of a particular fluid-structure partial
differential (PDE) model. This PDE fluid-structure system consists of a three- dimensional Stokes
flow, coupled to a two-dimensional plate equation. This fluid- structure PDE interaction is
described by the generator of a strongly continuous semi- group. The coupling between the
respective PDE dynamics is accomplished via a bound- ary interface and is captured in said
semigroup generator by unbounded trace opera- tors. Despite this unbounded boundary trace coupling
between distinct parabolic and hyperbolic, analytic effects from the fluid PDE components propagate
onto the entire structure, to the extent that the semigroup of the entire PDE exhibits a
quantifiable measure of Gevrey class regularity. This result thus provides decent affirmation of a
conjecture of the late Igor Chueshov.

---

The Effect of Higher-order Dissipation on Solutions of the Generalized
Korteweg-de Vries Equation
Jerry Bona, University of Illinois Chicago

---

The 2D Boussinesq Equations with Vertical Dissipation in a Bounded Domain
Chongsheng Cao, Florida International University

Boussinesq equations are mathematical models of buoyancy driven flows. In this talk we first
introduce the Boussinesq equations, then, we establish the global in time existence of classical
solutions to the 2D anisotropic Boussinesq equations with vertical dissipation in a bounded domain.
The results are similar to the one in whole space or
periodic domain. Here we need to deal with boundary layer problems.

---

Inviscid Limit from Navier-Stokes to BV Solutions of Compressible Euler Equations
Geng Chen, University of Kansas

In the realm of mathematical fluid dynamics, a formidable challenge lies in establishing
inviscid limits from the Navier-Stokes equations to the Euler equations. The pursuit of
solving this intricate problem, particularly concerning singular solutions, persists in both
compressible and incompressible scenarios. In particular, compressible Euler equations
are a typical system of hyperbolic conservation laws, whose solution forms shock waves
in general.
In this talk, we will discuss the recent proof on the unique vanishing viscosity limit
from Navier-Stokes equations to the BV solution of compressible Euler equations, for
the general Cauchy Problem. Moreover, we extend our findings by establishing the wellposedness
of such solutions within the broader class of inviscid limits of Navier-Stokes
equations with locally bounded energy initial values. This is a joint work with Kang
and Vasseur, which can be found on arXiv:2401.09305.
The uniqueness and L2 stability of Euler equations, done by Chen-Krupa-Vasseur,
will also be discussed in this talk.

---

Theory for a Higher-order Water Wave Model
Hongqiu Chen, University of Memphis
Considered here is a class of higher-order models for the unidirectional propagation of small
amplitude long waves on the surface of an ideal fluid. Namely,
ηt + ηx − γ1βηxxt + γ2βηxxx + δ1β2ηxxxxt + δ2β2ηxxxxx

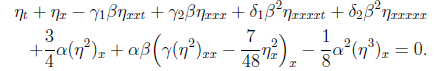
It was derived in [1], where η = η(x, t) is the deviation of the free surface from its rest
position at the point corresponding to x at time t. The two physical parameters α, β > 0 are small
compared to one and the Stokes’ number S = α/β is of order one. The five parameters γ₁, γ₂, δ₁, δ₂
and γ are not arbitrary. All restrictions are spelled out in detail in [1].
The pure initial-value problem for (1) in which the initial data

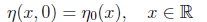
is viewed as known. In this talk, we show that if the parameters γ₁ and δ₁ appearing in front of
the ηₓₓt- and ηₓₓₓₓt-terms are positive, and if the initial data lies in the L₂- based Sobolev
space Hˢ(R) for s ≥ 1, then the initial-value problem (1)-(2) is locally well-posed in Hˢ(R).
Moreover, if γ = ⁷ , the well-posedness if global.
References
[1] J. L. Bona, X. Carvajal, M. Panthee and M. Scialom, Higher-order Hamiltonian model for unidi-
rectional water waves, J. Nonlinear Science 28 (2018), 543–577.

---

Structural Implication of Constant Vorticity to Three-dimensional Internal Waves
Ming Chen, University of Pittsburgh

It is known that in many physical regimes, water waves beneath vacuum that have constant vorticity
are necessarily two dimensional. The situation is more subtle for internal waves that traveling
along the interface between two immiscible fluids. When the layers have the same density, there is
a large class of explicit steady waves with constant vorticity that are three-dimensional in that
the velocity field is pointing in one horizontal direction while the interface is an arbitrary
function of the other horizontal variable. We prove that every three-dimensional traveling internal
wave with bounded velocity for which the vorticities in the upper and lower layers are nonzero,
constant, and parallel must belong to this family. If the densities in each layer are distinct,
then in fact the flow is fully two dimensional. This is a joint work with Lili Fan, Samuel Walsh,
and Miles Wheeler.

---

Ill-posedness Issues for Fluid Equations
Mimi Dai, University of Illinois Chicago

The mathematical theory of incompressible fluids still poses challenges for us today. The very
basic question of well-posedness remains open for many fluid equations, in- cluding the
Navier-Stokes equation (NSE) and other related systems. We will discuss some recent progress in the
effort to understand this classical problem by exploring ill- posedness phenomena, with an emphasis
on the construction of pathological solutions
which either violate uniqueness or develop finite time singularity.

---

Stokes Equations with Variable Coefficients and Applications
Hongjie Dong, Brown University

I will discuss some recent work on nonstationary Stokes equations with rough and
possibly unbounded coefficients. We obtained both interior and boundary estimates for
the velocity with minimal assumptions on the pressure term. Some applications to the
Navier-Stokes equations will be mentioned.

---

Stability of Close-to-Couette Shear Flows in a Finite Channel
Siming He, University of South Carolina

In this talk, I will present a threshold theorem for the 2D Navier-Stokes equations posed on the
periodic channel, supplemented with Navier boundary conditions. The initial datum is taken to be a
suitable perturbation of a shear flow that is close to the Couette flow. For such a datum, we prove
nonlinear enhanced dissipation and inviscid damping for the resulting solution. The principal
innovation is to capture quantitatively the inviscid damping, for which we introduce a new Singular
Integral Operator (SIO). We combine the SIO with the hypocoercivity functional to derive the
stability result.
This is joint work with Jacob Bedrossian, Sameer Iyer, and Fei Wang.

---

Optimal Control for Suppression of Singularity in Chemotaxis
Weiwei Hu, University of Georgia

In this talk, we discuss the problem of optimal control design for suppression of
singularity via flow advection in chemotaxis modeled by the Patlak-Keller-Segel (PKS) equations. It
is well-known that for the system without advection, singularity of the solution may develop at
finite time. Specifically, if the initial condition is above certain critical threshold, the
solution may blow up at finite time by concentrating positive mass at a single point. In this talk,
we will first address the global regularity and stability of the PKS system in the presence of flow
advection in a bounded domain, by using a semigroup approach. Then we focus on the design of an
optimal flow field for suppressing such singularities. Rigorous theoretical framework and numerical
experiments will be presented to demonstrate the ideas.

---

A Framework for Approximation by Reducing Algebraic Degree, with Applications to the 2D Kuramoto-Sivashinsky Equations and 3D Navier-Stokes Equations
Adam Larios, University of Nebraska-Lincoln

This talk presents a novel framework aimed at approximating the 2D Kuramoto- Sivashinsky equations
(KSE) and the 3D Navier-Stokes equations (NSE) by reducing the algebraic degree of their governing
equations. Building on the insights from work by Kostianko, Titi, and Zelik, which highlighted
limitations of standard regularizations for the KSE, our framework takes a different approach. This
method offers a stable alternative to traditional regularization techniques, which have been shown
to destabilize systems like the KSE, or require modifications to the boundary conditions or
derivative order of the NSE. Our approach retains essential dynamical features while ensuring
global well-posedness. To the best of our knowledge, this is the first globally well-posed PDE
system which approximates solutions to the 2D KSE (which is not known to be globally well-posed).
The talk will outline the theoretical foundation of this algebraic degree reduction, which we call
“calming,” and its application to both the KSE and NSE. We also show recent computational
simulations which indicate that the analytical
convergence rates we found are sharp.

---

Limiting Configurations for Solutions to the 1D Euler Alignment System
Trevor Leslie, Illinois Institute of Technology

The Euler Alignment system is a hydrodynamic PDE version of the celebrated Cucker- Smale ODE’s of
collective behavior. Together with Changhui Tan (University of South Carolina), we developed a theory of weak solutions in 1D, which provides a uniquely determined way to evolve the dynamics after a blowup. Inspired by Brenier and Gre- nier’s work on the pressureless Euler equations, we show that the dynamics of interest are captured by a nonlocal scalar balance law, the unique entropy solution of which we generate through a discretization involving the ”sticky particle Cucker-Smale” system. In this talk, we will discuss the formation of clusters of mass in the Euler Alignment sys- tem, and we will describe how to predict these clusters using the flux from the associated scalar balance law.

---

Thermodynamics and Temperature Effects for Chemical Reaction Dynamics
Chun Liu, Illinois Institute of Technology

In this talk, I will discuss the non equilibrium thermodynamics for various evolution systems
arising from applications in physics and biology. In particular, I will extend the energetic
variational approaches to non-isothermal situations and forces on the modeling
and analytical issues related to temperature effects.

---

Well-posedness of Mild Regularizations of Active Scalar Equation in Borderline Regularity Settings
Vincent Martinez, CUNY Hunter College

We study dissipative perturbations of the 2D generalized surface quasi-geostrophic (gSQG)
equations. This family contains the 2D Euler equations in vorticity form at one endpoint, an active
scalar equation whose constitutive law relates the velocity with the scalar with a loss of one
derivative, and contains the SQG equation at its midpoint. Recent work of Bourgain & Li, Elgindi &
Masmoudi, Cordoba & Zoroa-Martinez, and Jeong & Kim have established ill-posedness of this family
at critical regularity. This work considers a mild perturbation of the gSQG equation which recovers
well-posedness, but instantaneously confers a mild degree of regularity. This work is in
contradistinction with strongly dissipative perturbations, which instantaneously confer Gevrey
regularity and recover well-posedness at critical regularity (Jolly, Kumar, M 2021), and inviscid
regularization, which do not regularize solutions, but nevertheless recover local well- posedness
at critical regularity (Chae, Wu 2010). We show that in this intermediate regime that one may
recover local well-posedness at borderline Sobolev regularity, as well as a global existence theory
at the 2D Euler endpoint. Moreover, we provide a general existence theory for an entire class of
such perturbations that is effectively sharp in light of the recent ill-posedness results. This is joint work with A. Kumar (Florida
State University).

---

Intermittent Weak Solutions of the 3D Euler Equations
Matthew Novack, Purdue University

In this talk, I will present a series of recent works, in part joint with H. Kwon, V. Giri, and V.
Vicol. The common theme throughout is that the weak solutions we construct are intermittent; that
is, they display deviations from the scaling laws predicted by Kolmogorov’s 1941 theory of
turbulence. The techniques we have developed allow us to
(1) prove a ”strong” version of Onsager’s famous conjecture, and (2) construct solutions
to 3D Euler with well-defined helicity which is not conserved.

---

Eulerian Dynamics with Nonlinear Velocity Alignment
Changhui Tan, University of South Carolina

The Euler-alignment system describes the collective behaviors of animal swarms. In this talk, we
introduce a new type of alignment interaction that depends nonlinearly on velocity. We explore the
asymptotic flocking and alignment behaviors. Notably, the introduction of nonlinearity yields a
spectrum of distinctive asymptotic behaviors. Moreover, we present a rigorous derivation of our
system from a kinetic flocking model.
This is joint work with McKenzie Black.

---

Hyperbolic and Mixed-type Problems in Gas Dynamics and Geometry
Dehua Wang, University of Pittsburgh

We shall consider the hyperbolic and mixed-type problems arising in gas dynamics and geometry. In
particular, the transonic flows past obstacles and in nozzles as well as
the isometric embedding in geometry will be discussed.

---

Kinetic Schauder Estimates with Time-irregular Coefficients and Uniqueness for the Landau Equation
Weinan Wang, University of Oklahoma

We prove a Schauder estimate for kinetic Fokker-Planck equations that requires only H¨older
regularity in space and velocity but not in time. As an application, we deduce a weak-strong
uniqueness result of classical solutions to the spatially inhomogeneous Landau equation beginning
from initial data having H¨older regularity in x and only a logarithmic modulus of continuity in v.
This replaces an earlier result requiring H¨older
continuity in both variables. This is joint with Chris Henderson.

---

Non-uniqueness in Law of the Surface Quasi-geostrophic Equations: the Case of Linear Multiplicative Noise
Kazuo Yamazaki, University of Nebraska-Lincoln

Convex integration technique applied on stochastic PDEs has caught much atten- tion recently. The
surface quasi-geostrophic equations have been investigated in the physics community due to its wide
applications in geophysics, atmospheric sciences, and meteorology. Mathematically, the surface
quasi-geostrophic equations in momentum formulation consist of two nonlinear terms, besides the
pressure term, that cannot be written in a divergence form; additionally, it is one derivative more
singular than the nonlinear term of the Navier-Stokes equations. These issues bring about multiple
diffi- culties upon trying to employ the convex integration technique to the stochastic surface
quasi-geostrophic equations in momentum formulation forced by linear multiplicative
noise. We overcome these difficulties and prove its non-uniqueness in law.

---

Homogeneous Solutions of Stationary Incompressible Navier-Stokes Equations with Singular Rays
Xukai Yan, Oklahoma State University

In 1944, Landau discovered a three parameter family of explicit (-1)-homogeneous solutions of 3D
stationary incompressible Navier-Stokes equations with precisely one singularity at the origin.
These solutions, now called Landau solutions, are axisymmetric and has no swirl. In 1998 Tian and
Xin proved that all (-1)-homogeneous axisymmetric solutions with one singularity are Landau
solutions. In 2006 Sverak proved that all (- 1)-homogeneous solutions smooth on the unit sphere
are classified as Landau solutions. This talk focuses on (-1)-homogeneous solutions of 3D incompressible stationary NSE with finitely many singular rays. I will first discuss the existence and classification of such
solutions that are axisymmetric with two singular rays passing through the north and south poles.
We classify all such solutions with no swirl and then obtain existence of nonzero swirl solutions
through perturbation methods. I will then describe the asymptotic expansions of such solutions near
a singular ray. I will also establish the asymptotic stability for some of the axisymmetric
no-swirl solutions we obtained, and talk about some anisotropic Caffarelli-Kohn-Nirenberg type
inequalities we derived and applied in the study. This talk is based on joint works with Li Li and Yanyan Li.

---

Stability of a System of Balance Laws with Dynamic Boundary Flux
Kun Zhao, Tulane University

This talk is oriented around a system of balance laws in one space dimension, which is transformed
from a reaction-diffusion-advection model of chemotaxis and bears a structural resemblance to the
compressible Navier-Stokes equations. The balance law system is placed in a finite interval with
time-dependent Neumann boundary condition for one of the unknown functions and homogeneous
Dirichlet boundary condition for the other. By combining a relative entropy of Kullback-Leibler
type and Hˢ-based energy method, it is shown that classical solutions to the initial-boundary value
problem exists globally in time and converge to equilibrium states, determined by the
initial/boundary conditions or one of the system parameters, as time goes to infinity. There is no
smallness restriction on the initial data.

---

Iterative Projection Method for Unsteady Navier-Stokes Equations with High Reynolds Numbers
Xiaoming Zheng, Central Michigan University

The convectional projection method attempts to project the intermediate velocity to the divergence
free space only once per time step. However, such a velocity is not genuinely divergence free in
the general practices, which can yield large errors when the Reynolds number is high. The new
method iterates projections in each time step with the proper convection form and parameters. The
new method has several significant improvements over the conventional one both theoretically and
practically. First, when the iterative projections are fully convergent in each time step, the
numerical velocity is weakly divergence free, and the stability and error estimate are rigorously
proven. Second, numerical simulations show that with rather relaxed stopping criteria which
require only a few iterations at each time step, the numerical solution preserves stability and
accuracy for high Reynolds numbers, where the convectional projection method would fail.
Furthermore, this method retains the efficiency of the traditional projection method by decoupling
the velocity and pressure fields. Three dimensional simulations with Taylor-Hood P2/P1 finite
elements are presented to demonstrate the performance
and efficiency of this method.