My research includes theoretical and numerical analysis for free boundary problems with real-world applications. In particular, I mainly focus on the topics of stability and bifurcation since these two topics are of practical importance in applications. The following are some projects I did in my Ph.D. studies:
1. Tumor growth model with a time delay in cell proliferation
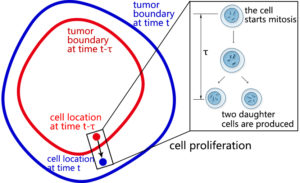A new PDE model is proposed for non-radially symmetric tumor growth with a time delay in cell proliferation. The time delay represents the time taken for cells to undergo replication. The model is a coupled system of an elliptic equation, a parabolic equation, and a backward ordinary differential equation. It also incorporates the cell location under the presence of time delay (see left figure, cell location changes in the period of time delay), with the tumor boundary as a free boundary. For the new model, we successfully carried out the stability and bifurcation analysis (see my publication [1] and [2]).
2. Atherosclerosis
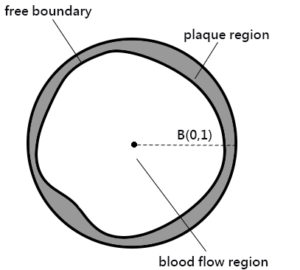
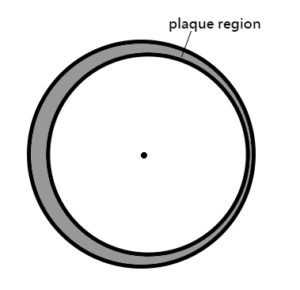
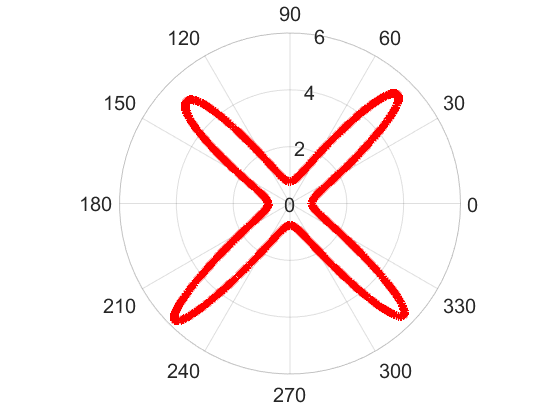
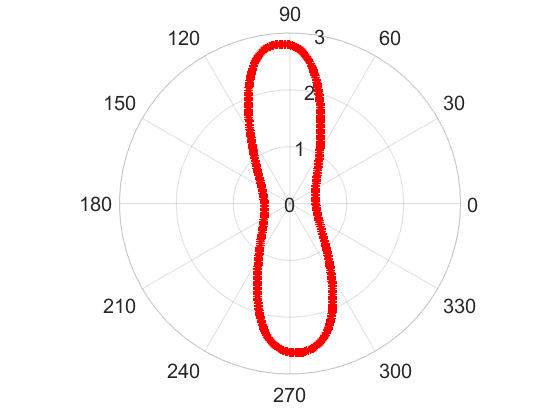
We studied the bifurcation for a highly nonlinear and highly coupled free boundary PDE system describing the growth of arterial plaque. The model involves high density lipoprotein cholestrols, low density lipoprotein cholestrols, macrophage cells and foam cells. As shown in the upper left figure, we consider the cross section of an artery. There are plaque region and blood flow region, with the interface separating these two regions being a free boundary. Finite branches of symmetry-breaking stationary solutions were established for the model (see my publication [3]). Moreover, we showed that the first bifurcation point for the system corresponds to the mode n=1 (see my publication [4]), which would result in the solution pattern shown in the upper right figure. As some arterial plaque is often accumulated more on one side of the artery, our bifurcation result can help to understand this phenomenon.
3. Solving free boundary systems by using neural networks
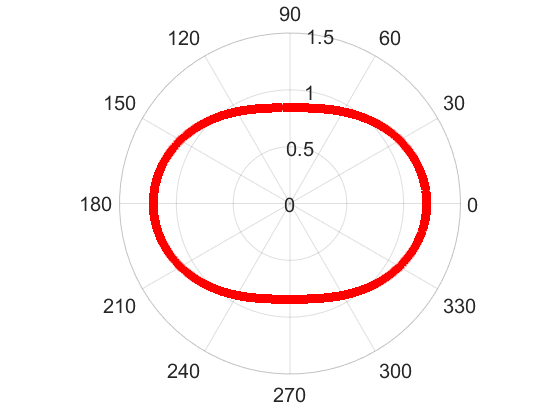
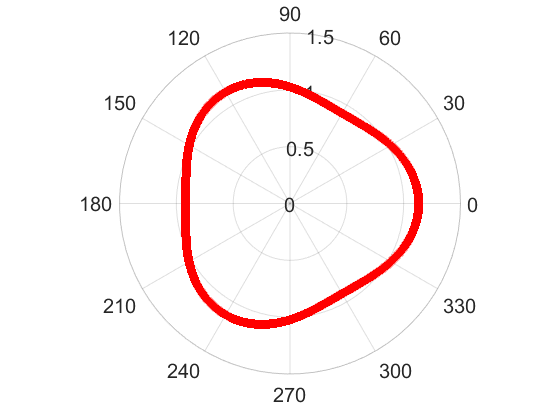
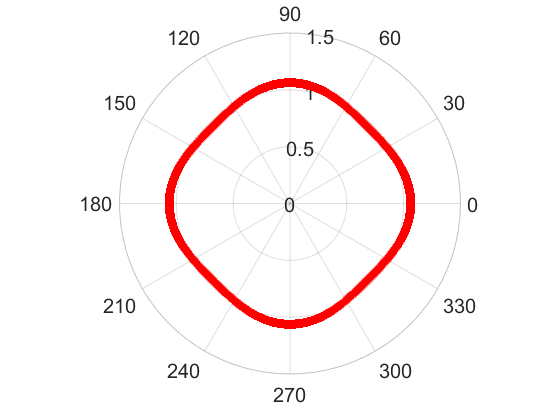
We proposed a novel numerical approach to solve free boundary systems based on boundary integral method and neural network discretization. In my publication [5], we applied this method to solve a modified Hele-Shaw problem with surface tension. The existence of numerical solutions was theoretically established under our new scheme. In the simulations, we first verified this approach on radially symmetric and known non-radially symmetric solutions. The following 4 figures show the shapes of symmetry-breaking solutions on n=2, n=3, n=4, and n=5 bifurcation branches. All these solutions can be fully characterized by the theoretical derivations and are recovered by our numerical method.
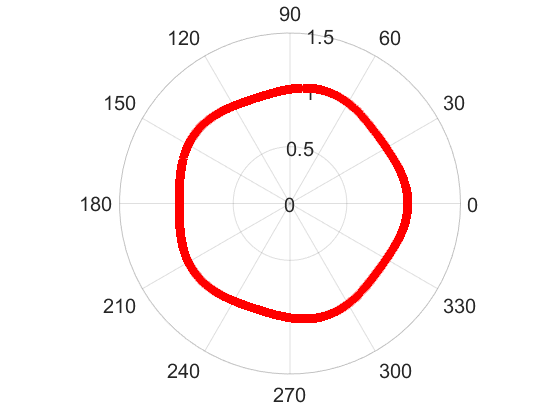
Moreover, we further verified the capacity of the new method by computing some non-radially symmetric solutions which are not characterized by any theories. In particular, we found the following fingering-like patterns.
