Second Edition, May 2015.

Corrections: There is now (as of October 2016) a corrected second printing of the second edition, available from Amazon.com and from Springer. The second printing fixes many typos in the first printing and also clarifies a few proofs in Chapter 9. If the acknowledgments section at the end of the preface mentions “additional input on the second printing of the second edition,” you have the corrected second printing.
Here is a list of errata to the first printing of the second edition: erratum. (These have been corrected in the second printing.)
Here is a revised version of Section 9.4: New9.4. (This has been incorporated into the second printing.)
Please send any additional corrections to me at bhall@nd.edu .
New features of second edition: The second edition maintains a key feature of the first edition, namely the use of matrix Lie groups instead of general Lie groups. This approach allows one to get started quickly without needing to develop the machinery of smooth manifolds. As in the first edition, I use the Baker-Campbell-Hausdorff formula in place of the more traditional Frobenius theorem to develop the deeper results about the relationship between groups and Lie algebras.
The new edition then adds a lot of new material on representation theory of semisimple Lie algebras and compact groups. I now give a full development of the representation theory of semisimple Lie algebras, including the introduction of the universal enveloping algebra and a proof of the Poincare-Birkhoff-Witt theorem. I also have a mostly new chapter developing additional properties of the representations, including complete reducibility (algebraic proof), the Weyl character formula, the Weyl dimension formula, and the Kostant multiplicity formula.
Finally, the second edition adds a new section on the structure and representations of compact Lie groups. The first chapter in this section develops the torus theorem, the Weyl integral formula, and the structure of the Weyl group. The second chapter in the section then uses these tools to develop the theorem of the highest weight (classifying the representations) from the compact group point of view. The last chapter then examines the fundamental group of compact Lie groups from two different perspectives, one using an inductive approach (for the classical groups) and the other using the structure of the roots and the kernel of the exponential mapping.
I have also included many more images than in the first edition, including several in color.
Questions and corrections are always encouraged: bhall@nd.edu.
Table of contents for the second edition: TOC.
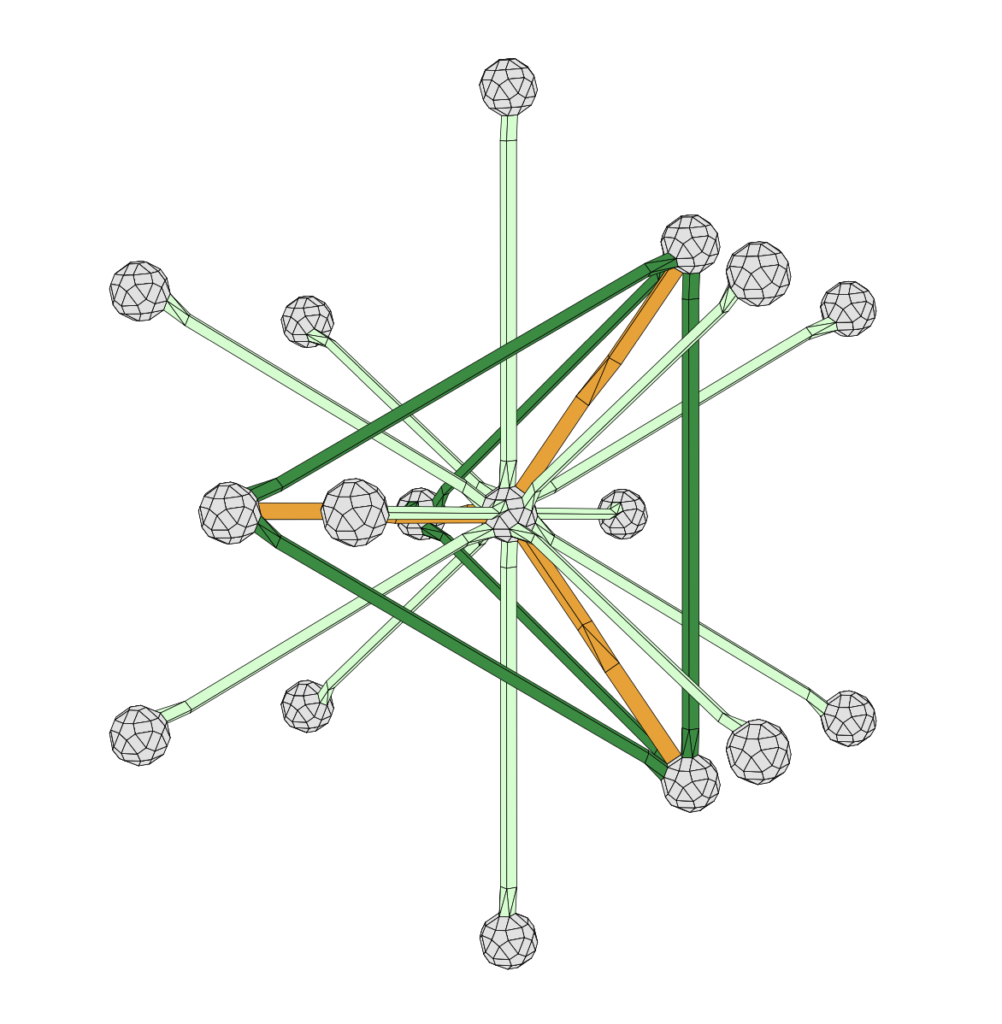
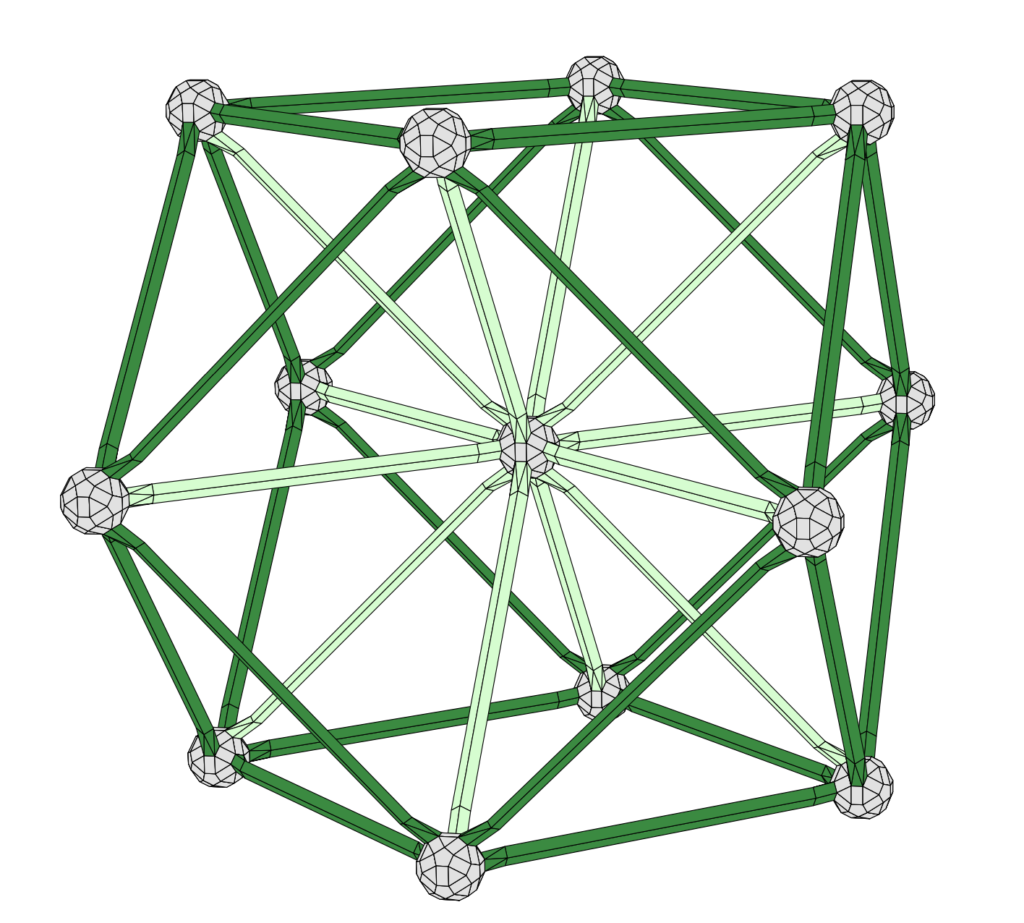
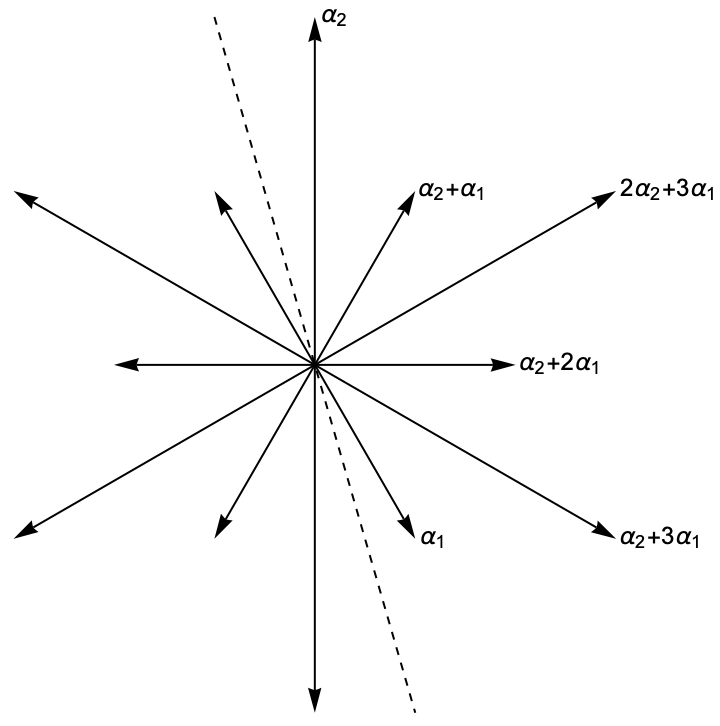
Root systems in the Zometool system: As in the first edition, the book includes color images of root systems in rank three, created using the Zometool system zometool.com . I have also developed a detailed set of instructions for constructing the root systems and related objects (fundamental weights, root lattice, weight lattice, etc.).
Instructions for building roots systems in Zometool: RootSystemsKit.