I consider myself a mathematical physicist, with the problems I work on usually motivated in some way by quantum physics. My thesis developed an extension of the Segal–Bargmann transform to compact Lie groups. This construction and the associated family of coherent states have been used extensively in the physics literature in connection with loop quantum gravity. The generalized Segal–Bargmann transform for compact Lie groups also has connections with geometric quantization and two-dimensional Yang–Mills theory.
I have also worked on various aspects of geometric quantization, including the connection between quantization and symplectic reduction. More recently, I have done work on two-dimensional Yang–Mills theory on surfaces, including the Makeenko–Migdal equation and the large-N limit.
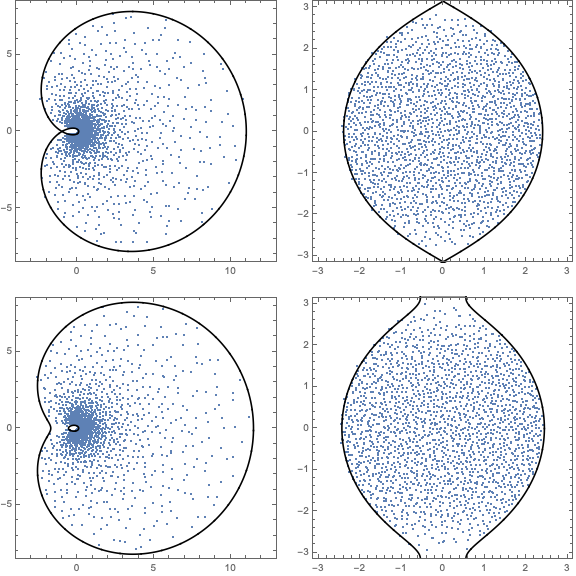
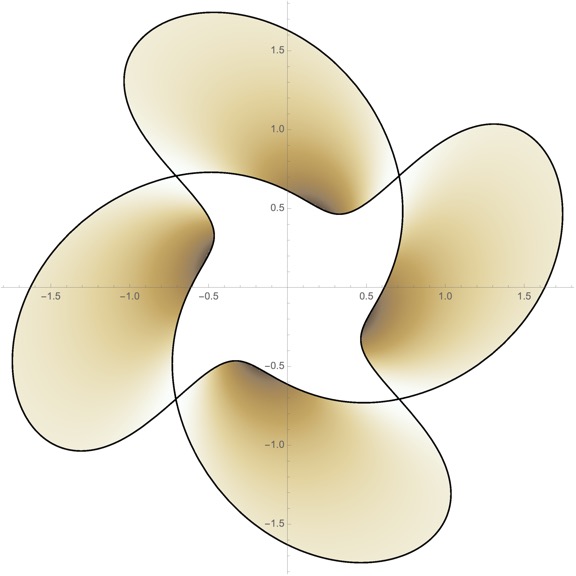
In the last few years, I have been working on random matrix theory and related models in free probability. In work with Bruce Driver and Todd Kemp of UCSD, I developed a new PDE method for computing the Brown measure of free random variables connected to Brownian motions. These Brown measures are the natural candidates for the limiting eigenvalue distributions of the corresponding random matrix models. Lately, I have been further developing this program in work with Ching Wei Ho (Academia Sinica in Taiwan) and Jonas Jalowy and Zakhar Kabluchko (Munster).