H. Gao*, J.-X. Wang, A Bi-fidelity Ensemble Kalman Method for PDE-Constrained Inverse Problems, Computational Mechanics
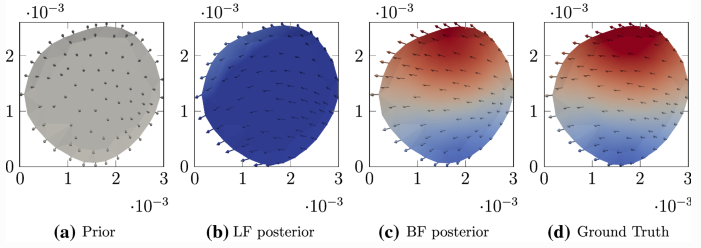
Mathematical modeling and simulation of complex physical systems based on partial differential equations (PDEs) have been widely used in engineering and industrial applications. To enable reliable predictions, it is crucial yet challenging to calibrate the model by inferring unknown parameters/fields (e.g., boundary conditions, mechanical properties, and operating parameters) from sparse and noisy measurements, which is known as a PDE-constrained inverse problem. In this work, we develop a novel bi-fidelity (BF) ensemble Kalman inversion method to tackle this challenge, leveraging the accuracy of high-fidelity models and the efficiency of low-fidelity models. The core concept is to build a BF model with a limited number of high-fidelity samples for efficient forward propagations in the iterative ensemble Kalman inversion. Compared to existing inversion techniques, salient features of the proposed methods can be summarized as follow: (1) achieving the accuracy of high-fidelity models but at the cost of low-fidelity models, (2) being robust and derivative-free, and (3) being code non-intrusive, enabling ease of deployment for different applications. The proposed method has been assessed by three inverse problems that are relevant to fluid dynamics, including both parameter estimation and field inversion. The numerical results demonstrate the excellent performance of the proposed BF ensemble Kalman inversion approach, which drastically outperforms the standard Kalman inversion in terms of efficiency and accuracy.

