Post by John Tipton, statistics graduate student with Mevin Hooten at Colorado State University, about work John and Mevin are doing with Jack Williams and Simon Goring.

“Big data” has very rapidly become a popular topic. What are big data? The concept of big data in statistics is the analysis of very large datasets with the goal of obtaining inference in a reasonable time frame. The paleoclimate world often has the opposite problem: taking small amounts of data and expanding to produce a spatially and temporally rich result while accounting for uncertainty. How do you take a handful of temperature observations and predict a temperature surface over 20,000 locations for a period of 73 years in the past? Perhaps some of the techniques used in big data analysis can help.

Figure 1. Four representative years of temperature records (ºC) from the historical fort network.

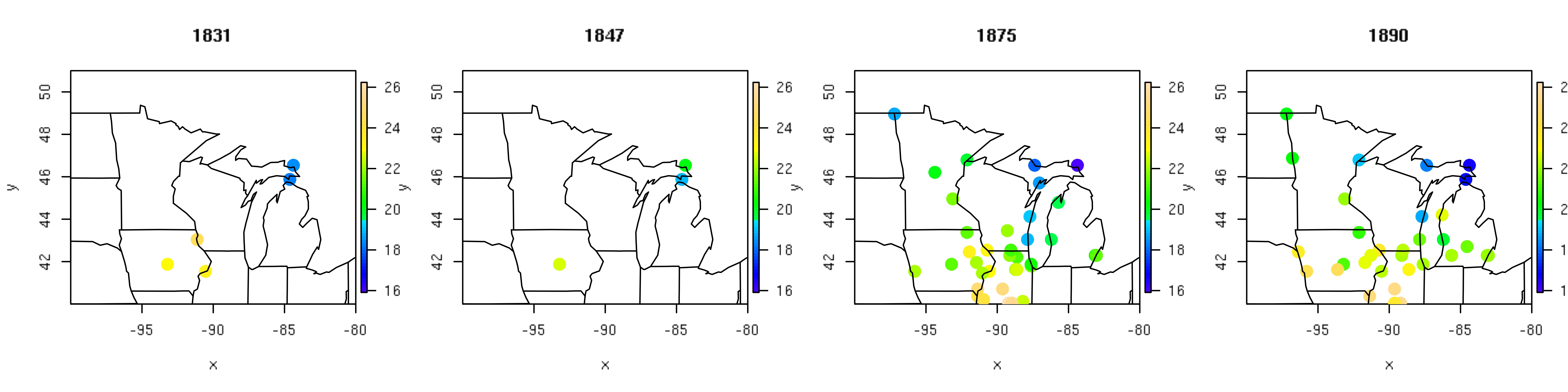
The U.S. fort data consist of temperature records from military forts in the Upper Midwest region of the United States from 1820-1893. A subset of these instrumental temperature records (Figure 1) illustrates the sparse nature of the historical U.S. fort data relative to the spatial area of interest, especially in the earlier two years (1831 and 1847). From the small set of temperature observations collected each year, we seek to reconstruct average July temperature at a fine grid of 20,000 prediction locations. Techniques such as optimal spatial prediction, dimension reduction, and regularization allow us to provide formal statistical inference for this very large underlying process using a relatively small set of observational data.

To ameliorate the sparsity of the fort data, we used patterns from recent temperature fields (i.e., PRISM products) as a predictor variables in a Bayesian hierarchical empirical orthogonal function regression that includes a correlated spatial random effect. A strength of this modeling technique is that the primary patterns of temperature should remain stable even though the magnitude might change (e.g., it will always be cooler in the north than in the south). Another characteristic of this methodology is that it allows for localized differences in prediction to arise through a correlated spatial random effect. The correlated spatial random effect is too computationally expensive to calculate using traditional methods so the effect is estimated using big data techniques. Specifically, any remaining correlation that ties the fort locations together beyond that predicted by combinations of the primary temperature patterns is approximated in a lower dimensional space. This greatly reduces the computational effort needed to fit the model. We also employ a type of model selection technique called regularization to borrow strength from years with more data. This results in predictions that are close to the historical mean when there are few observations in a given year, while allowing for more detailed predictions in years with more data. To make the model selection computationally feasible, we fit the model in a highly parallelized high performance cluster computing environment.

The use of big data techniques for large paleoclimate reconstruction allows for statistical estimation of climate surfaces with spatially explicit uncertainties. Results of the mean July temperature for the subset of four years are shown in Figure 2, while the associated spatially explicit uncertainties are shown in Figure 3. These figures illustrate the strengths of the modeling techniques used. In the two earlier years, the predictions are similar to the historical mean with uncertainty increasing as a function of distance from observations. In the two later years with more data, the predictive surfaces have more spatial complexity and less associated uncertainty.

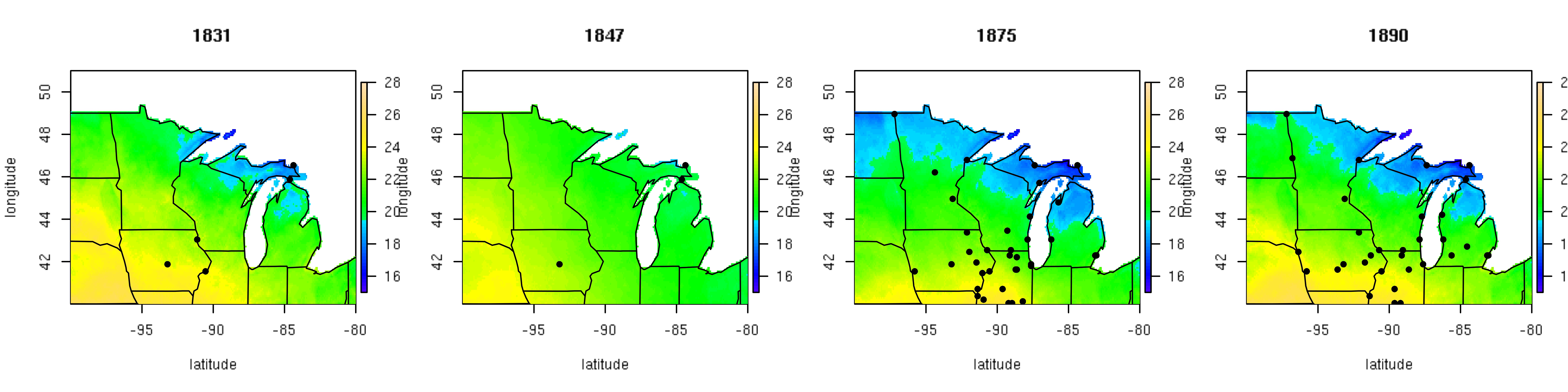
Figure 2. Reconstruction based on the posterior mean July temperature (ºC) for four representative years of the historical fort network.

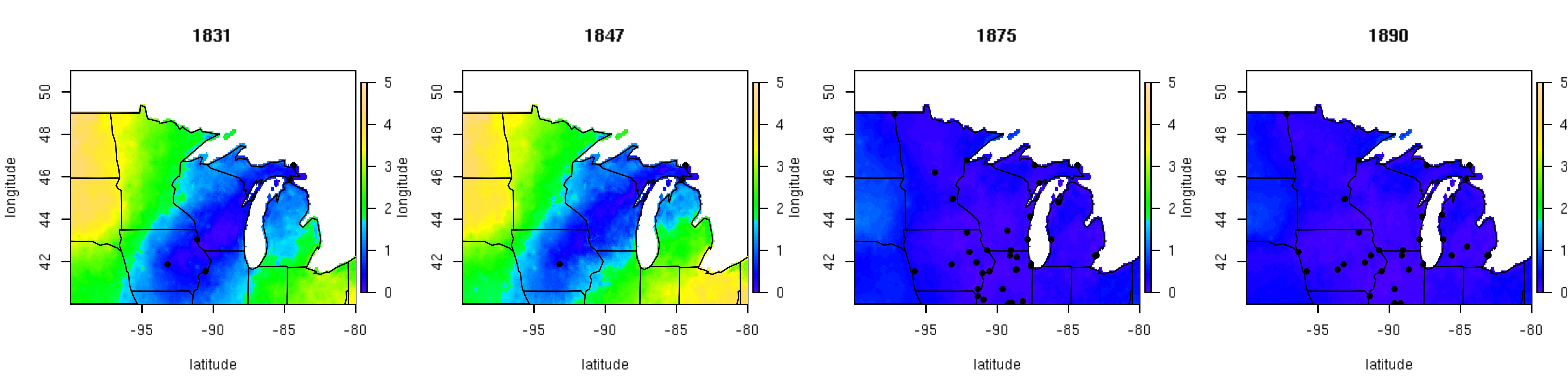
Figure 3. Posterior standard deviation surface of mean July temperature (ºC) for four representative years of the historical fort network.

By explicitly accounting for latent correlated spatial structure and moderating model complexity using regularization, spatio-temporal predictions of paleoclimate are improved. Furthermore, dig data techniques allow us to fit the statistical models in a reasonable time frame (i.e., on the order of days rather than weeks). The relatively small sample sizes commonly associated with paleoclimate data would not normally fall into the “big data” realm of analyses. However, the processes on which we seek inference are quite large, and thus “big data” techniques are tremendously helpful.