These questions show you that three common mathematical tasks at the roots of linear algebra and quantum mechanics are equivalent; the three tasks are:
- Diagonalization of a matrix.
- Minimization of a linear functional.
- Fourier transform of the matrix exponential
In what sense equivalent? In the sense that if you have performed any of these tasks you can translate the answer to the other task with little-to-no effort. The “answer” if it is a vector can be imagined to be a wavefunction, if it is an scalar, you should imagine it to be an energy or an eigenvalue. Most “work” in quantum mechanics falls into one of these three categories. One quick example of their inter-relations coming in handy is quantum phase estimation which is the (3)->(1) map. A main trick not on the list is Monte-Carlo which can be used to solve (2) and (3) as an integral approximation. It can be used for (1) as well which was the topic of recent research.
- Show how to exponentiate a matrix trivially, assuming it can be diagonalized (ie: assuming you know it’s eigenvalues and eigenvectors).
- Show that the vector v, which minimizes the “Ritz functional” of the matrix A,
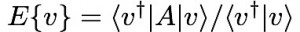, is the eigenvector of A with smallest eigenvalue. (HINT: assume eigen-decomposition of A). Side question: Show that E{v} is stationary ie: has derivative zero if and only if v is an eigenvector of A. - Show that the Fourier transform: G(\omega) = \int_-\infty^\infty exp(-iAt+i\omega t)dt where A is a Hermitian matrix, has poles (singularities etc.) at the eigenvalues of A. (hint use properties of Fourier transform and eigendecomposition of A)
