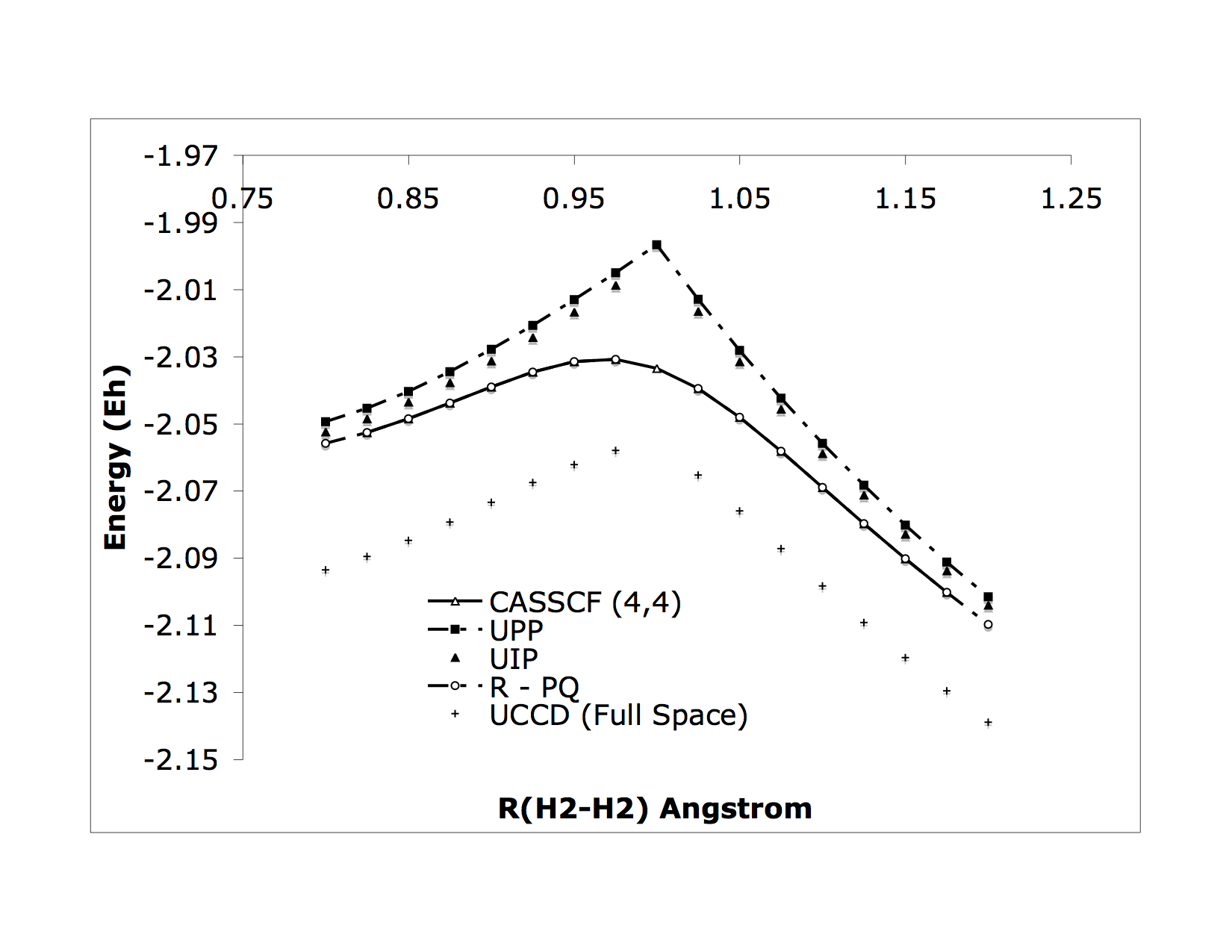
We’re interested in the application and development computational models for the properties of quantum or nearly quantum chemical systems from first principles. Although this field is very mature in terms of man-hours, it is riddled with nooks and crannies where very simple chemical problems are difficult or impossible to answer accurately, and we like to solve these problems. One example from our early work is bond making-breaking processes where we developed some sparse, orbital-optimized, high-rank coupled cluster methods to treat strong correlations:
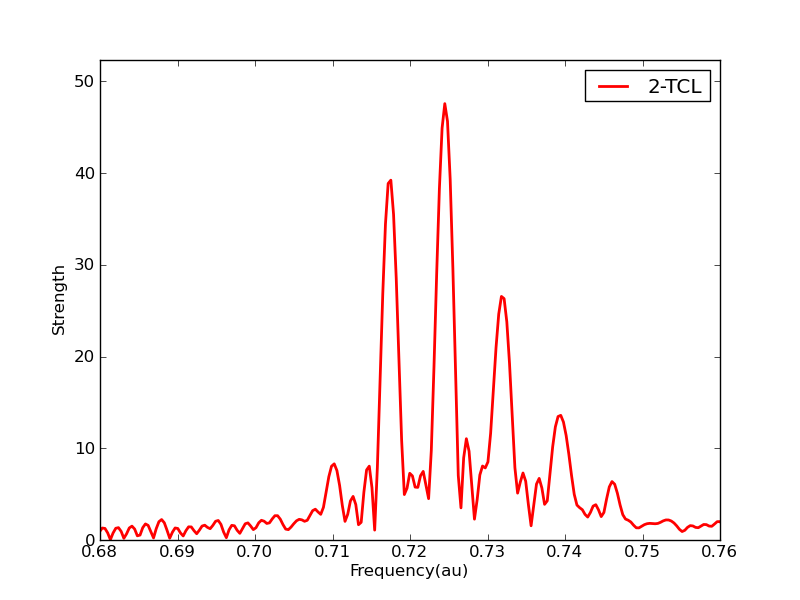
Excited states, and especially the dynamics of excited states are a huge challenge for quantum chemistry. At the time I am writing this it is not trivial to predict the absolute color of a dye using methods that we have available (TDDFT, ADC(N), EOM-CC, CIS(D), CASPT, etc.) although relative excited state energies can be well-behaved. At least some of the difficulty comes about from breakdown of the stationary state picture. Kasha’s rule tells us that excited states decay generically, but this very basic feature is missing from our models. So we are developing formalism to include these effects in excited states. For example this causes linear response peaks to have physical widths or vibronic progressions:
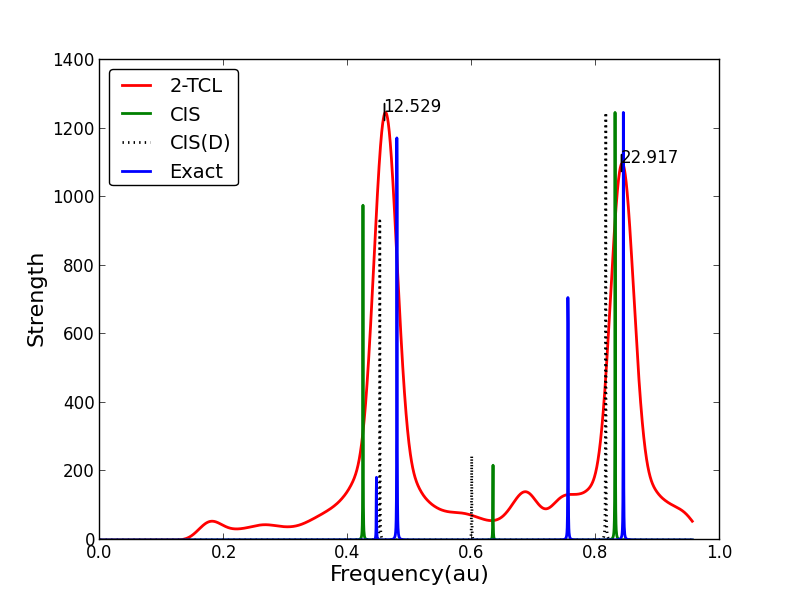
Interestingly we’ve found that the same theory is useful to treat electron correlation effects in excited states. Below you see a linear response spectrum made from a dynamic perturbation theory, vs. normal methods:
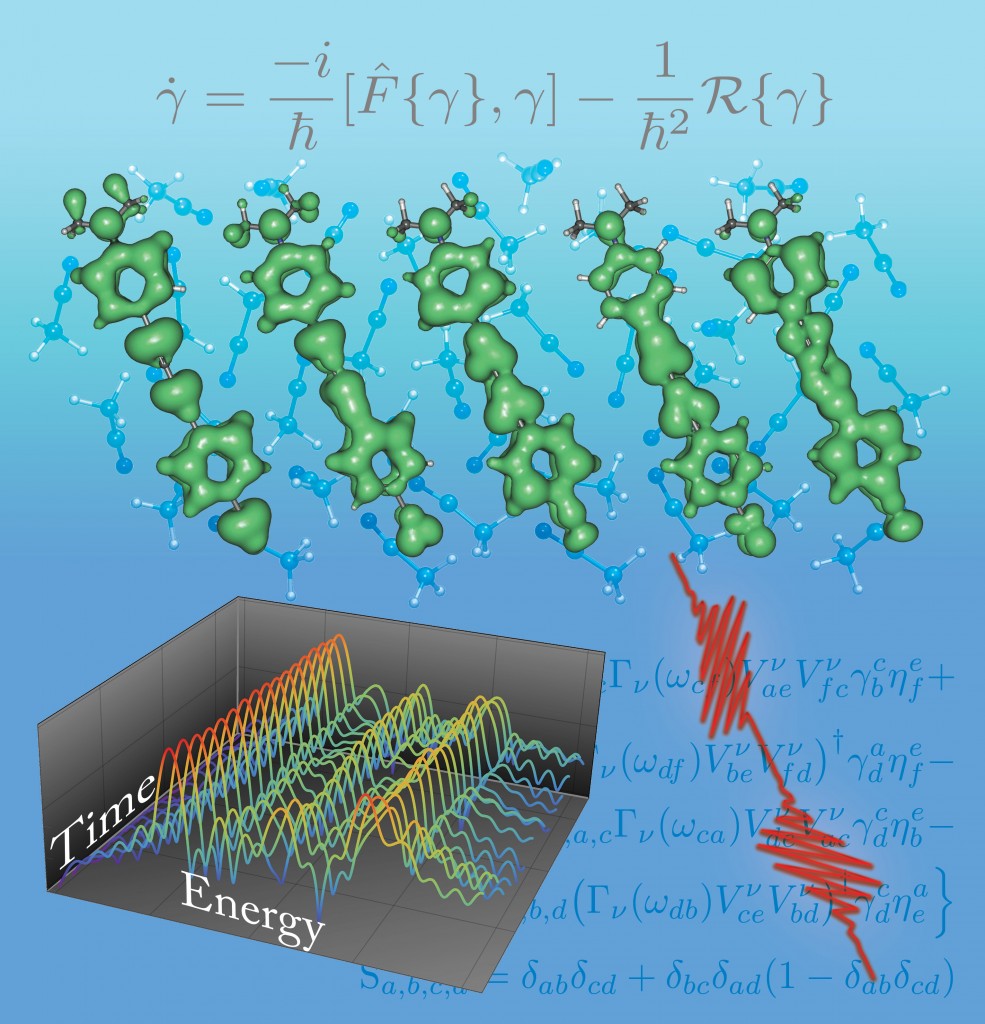
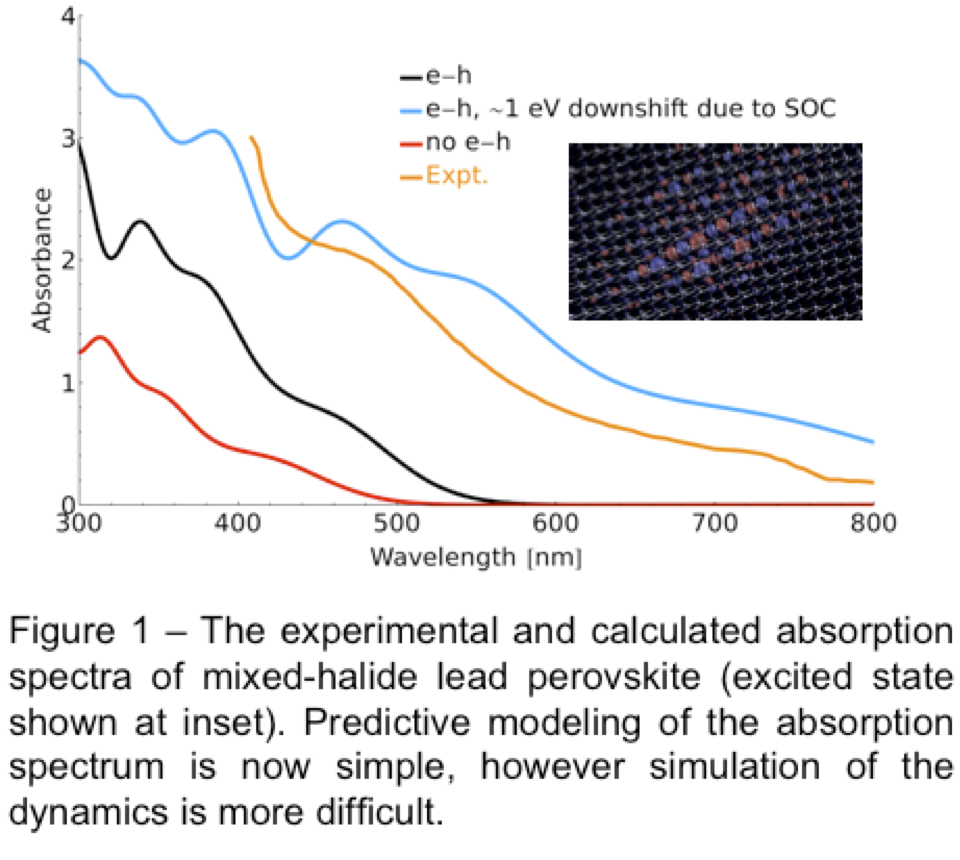
Nowadays we are applying these theories to much larger systems, and exploring other effects like exchange screening which lead to intense modification of absorption spectra: