Personal hero and noted banjo enthusiast Bill Miller often poses the following thought experiment to critique classical MD:
The zero point energy in the ~3000 wavenumber modes of water is more than 20 times larger than Kb*T at room temperature. If you gave these degrees of freedom their ZPE in classical MD that ZPE would leak into other modes, at the very least resulting in a high effective temperature.
In protein simulations this isn’t an immediate problem because high-frequency oscillators are frozen out by the SHAKE algorithm (to allow for large integrator timesteps) and given no zero point energy. Clearly it would be nicer to treat the quantum effects in the MD. People in this field know there are many, many ways to do this, usually based on some scheme to approximately integrate the path integral, but nothing as simple as running CHARMM or CPMD.
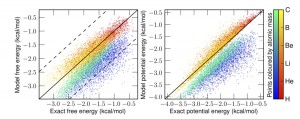
In this pre-print Ryan Alan and I propose an alternative: generate an effective force field which reproduces the density of the quantum system under the laws of classical statistical mechanics. We show such a potential exists, and that the map between the physical potential and the fictitious effective potential is unique. You can think of this like DFT for quantum MD, it takes a simulation which is easy to perform (classical MD/MC) and gives you the exact density. The catch is that you need to come up with this mapping that contains all the information about the difference between the quantum and classical effective potentials. (something like the problem of knowing the exact functional). We also numerically inverted that map for some low dimensional systems.