Readers familiar with the physics of open quantum systems have probably encountered a functional parametrization (ohmic, super-ohmic, etc.) for a thermal bath of linearly coupled, non-interacting harmonic oscillators. Physically motivating these models from the atomistic structure of a quantum material is a difficult and expensive semi-classical process, but the detailed structure of the bath can drastically alter short time population dynamics. The most satisfying procedure I am aware of consists of:
1) Performing a closed-dynamics (usually classical) simulation of quantum system and environment, somehow partitioning system and environment so you can monitor energy fluctuations of the system.
2) Taking the resulting energy fluctuation time-series constructing the real, symmetric classical correlation function.
3) Semi-classically extending this correlation function to obey the quantum conditions for causality and detailed balance while performing a Fourier transform to obtain the frequency dependent model for the harmonic bath.
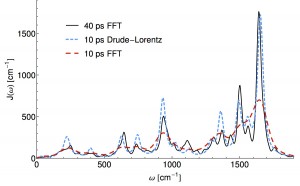
In terms of wall-time, step 1) is most expensive because something like ab-initio MD needs to be run for a length time going as the inverse frequency of the slowest bath mode (40ps or so) while sampling the quantum Hamiltonian in the classical environment. In this recent work Thomas Markovitch reduced by a factor of roughly 8 the required MD simulation time, by exploiting a sparse l1 signal processing technique (super-resolution). As an added bonus the l1 technique decomposes the spectral density into an analytical form which yields an analytic non-Markovian bath kernel. This is a step towards “black-box” baths which are more than three parameters of an Ohmic function. (ArXiv)