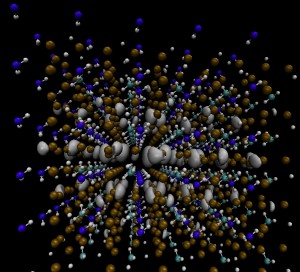
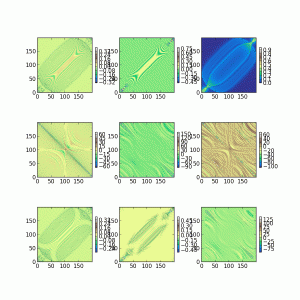
Members of the group enjoy the cartoon stylings of artist in residence Triet.
Author Archives: John
Come by and support our book drive!
Image
Triet’s Poster from ACTC.
She’s gotten a lot done this year. (dropbox pdf link)
Opportunities for Highly Motivated Postdocs.
If you feel you have a strong background in electronic structure theory and would like a challenging postdoctoral opportunity in method development, feel free to email me your CV.
Best-
John
Thanks Midwest Theory Organizers!
The group had a great time at the Midwest Theoretical Chemistry conference, thanks to Professors Shiozaki, Schatz Ratner, Seideman, Snurr, Szleifer, Reuter and Olvera!
Congratulations Nahee.
Undergraduate Nahee Kim has received a College of Science Summer Undergraduate Research Fellowship. (on behalf of her and the group, thanks college of science)
Congratulations Triet!
Triet Nguyen got an NSF graduate fellowship.
CONGRATULATIONS!
Random research image of the day.
Late Christmas gifts.
Welcome Postdoctoral Fellow Ravindra Nanguneri
Ravi is a UC Davis physics Ph.D. with a background studying metal oxides. He comes to us during a period of anomalously frigid weather in South Bend, but seems to be dealing with it cheerfully.
University’s Christmas present is Lab Space.
Welcome Grad Student Kun Yao
Kun is thinking about non-radiative relaxation, and temporarily desk-less until the group space is finished.
Jarrod’s work is featured on Phys.org.
Couldn’t be happier for him! The blurb is pretty digestible for non-experts.
http://phys.org/news/2013-10-feynman-wasnt-quantum-dynamics-ground.html
A Symposium for Polarizable Systems
Daniel Lambrecht and myself are organizing a symposium at the Denver 2015 ACS on the subject of electronic structure methods for simulating highly polarizable systems. Please contact one of us if you are interested in contributing a talk. Here is the poster summary:
“There are widespread technological applications for molecules which can readily accept and transform small packets of energy. Optoelectronic materials, molecular electronics, and photocatalysis speak to the technological impact of modeling such systems. At the same time, any rational advancement involves a firm understanding of fundamental processes such as energy and electron transfer, electron and nuclear dynamics, and electron-phonon interactions. Modeling the interactions of polarizable molecules with their environment therefore remains a challenge for modern electronic structure theory and represents an area of vibrant development. This symposium collects emerging methodologies for computing the properties of small-gap, polarizable materials in their ground and excited states. New phenomenological and ab-initio theories targeted at these systems are welcome contributions to this symposium, including developments in embedding approaches, excited state theories and electronic dynamics. State-of-the art applications of first principles approaches theory used to interpret, rationalize and guide experiment are also invited. The tools discussed are useful for studying charge and energy collection and transport on lengths ranging between atomic systems and the nanoscale.”
LaTeXIT as a web service.
So cool.
http://tex.sh/tex/$<latex goes here>$.pngTriet’s Poster from ACS
Triet gave a poster at ACS about our first month of work. It looks pretty good (pdf link)
Wecome to Undergraduate Nahee Kim
Nahee is a Junior in Notre Dame’s college of sciences and has some experience with Wavelets. She’s going to be working on some signal processing in the group.
Data’s coming in.
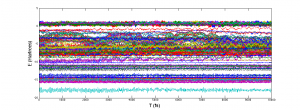
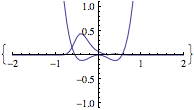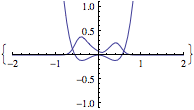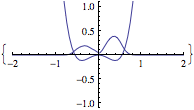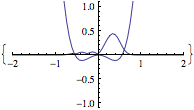
Triet is a very good summer student, and she’s studying the classical noise that electrons experience after just 2 weeks of group history. The fluctuations she captured and plotted below will be used to characterize dephasing between electrons within a single molecule. Looking at the magnitude of these single electron energy fluctuations at 300K, we expect to be busy for a long time building dephasing models and understanding how they change photochemistry and excited state dynamics.
Our equipment has arrived!
Bath models made more cheaply and more physically
Readers familiar with the physics of open quantum systems have probably encountered a functional parametrization (ohmic, super-ohmic, etc.) for a thermal bath of linearly coupled, non-interacting harmonic oscillators. Physically motivating these models from the atomistic structure of a quantum material is a difficult and expensive semi-classical process, but the detailed structure of the bath can drastically alter short time population dynamics. The most satisfying procedure I am aware of consists of:
1) Performing a closed-dynamics (usually classical) simulation of quantum system and environment, somehow partitioning system and environment so you can monitor energy fluctuations of the system.
2) Taking the resulting energy fluctuation time-series constructing the real, symmetric classical correlation function.
3) Semi-classically extending this correlation function to obey the quantum conditions for causality and detailed balance while performing a Fourier transform to obtain the frequency dependent model for the harmonic bath.
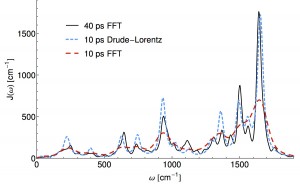
In terms of wall-time, step 1) is most expensive because something like ab-initio MD needs to be run for a length time going as the inverse frequency of the slowest bath mode (40ps or so) while sampling the quantum Hamiltonian in the classical environment. In this recent work Thomas Markovitch reduced by a factor of roughly 8 the required MD simulation time, by exploiting a sparse l1 signal processing technique (super-resolution). As an added bonus the l1 technique decomposes the spectral density into an analytical form which yields an analytic non-Markovian bath kernel. This is a step towards “black-box” baths which are more than three parameters of an Ohmic function. (ArXiv)
Post-doctoral Position Available
Ph.D. students with a strong background in numerical computation and chemical physics are encouraged to send a C.V. along with a brief email describing their goals and experience to john(dot)parkhill(at)gmail(dot)com.
Classical Force-Fields which Reproduce Equilibrium Quantum Distributions
Personal hero and noted banjo enthusiast Bill Miller often poses the following thought experiment to critique classical MD:
The zero point energy in the ~3000 wavenumber modes of water is more than 20 times larger than Kb*T at room temperature. If you gave these degrees of freedom their ZPE in classical MD that ZPE would leak into other modes, at the very least resulting in a high effective temperature.
In protein simulations this isn’t an immediate problem because high-frequency oscillators are frozen out by the SHAKE algorithm (to allow for large integrator timesteps) and given no zero point energy. Clearly it would be nicer to treat the quantum effects in the MD. People in this field know there are many, many ways to do this, usually based on some scheme to approximately integrate the path integral, but nothing as simple as running CHARMM or CPMD.
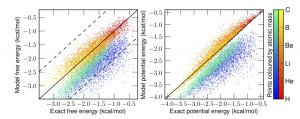
In this pre-print Ryan Alan and I propose an alternative: generate an effective force field which reproduces the density of the quantum system under the laws of classical statistical mechanics. We show such a potential exists, and that the map between the physical potential and the fictitious effective potential is unique. You can think of this like DFT for quantum MD, it takes a simulation which is easy to perform (classical MD/MC) and gives you the exact density. The catch is that you need to come up with this mapping that contains all the information about the difference between the quantum and classical effective potentials. (something like the problem of knowing the exact functional). We also numerically inverted that map for some low dimensional systems.
McClean’s Clock Variational Principle
In the time between finishing my post-doc and beginning the group I’ve been indulging my appetite for random quantum ideas outside of the electronic structure realm. Jarrod McClean came up with this pretty wild adaptation of quantum computing’s ancilla concept to do quantum dynamics. The approach (which we cast as a version of the quantum time-dependent variational principle) has some interesting features, and we eventually managed to do parallel in time dynamics with it. (arXiv)
Welcome to Summer Student Triet Nguyen!
Triet S. Nguyen comes from Dallas where she studied nanotubes for drug delivery as an undergraduate in the Lab of Prof. Steven O. Nielsen with the assistance of Dr. Udayana Ranatunga. She originally hails from Saigon, and is interested studying quantum aspects of energy transport. Her summer study is supported by generous fellowship funding from The Department of Chemistry at Notre Dame, and she can be temporarily found in COMSEL devouring online coursework and filling Notre Dame CRC queue with chemical simulations. Welcome Triet.
Some new code in the Bitbucket.
By email request, I’ve pushed some Mathematica code into the Bitbucket for generating coupled cluster equations and code.
Congratulations Amigos!
It’s been a good week or two for good scientists. Alan got his well-deserved tenure. All around stand-up guy and quantum chemist Greg Beran got tenure. (Congratulations amigos)
Questions for beginners.
- Diagonalization of a matrix.
- Minimization of a linear functional.
- Fourier transform of the matrix exponential
- Show how to exponentiate a matrix trivially, assuming it can be diagonalized (ie: assuming you know it’s eigenvalues and eigenvectors).
- Show that the vector v, which minimizes the “Ritz functional” of the matrix A,
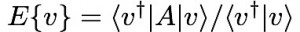 , is the eigenvector of A with smallest eigenvalue. (HINT: assume eigen-decomposition of A). Side question: Show that E{v} is stationary ie: has derivative zero if and only if v is an eigenvector of A.
, is the eigenvector of A with smallest eigenvalue. (HINT: assume eigen-decomposition of A). Side question: Show that E{v} is stationary ie: has derivative zero if and only if v is an eigenvector of A. - Show that the Fourier transform: G(\omega) = \int_-\infty^\infty exp(-iAt+i\omega t)dt where A is a Hermitian matrix, has poles (singularities etc.) at the eigenvalues of A. (hint use properties of Fourier transform and eigendecomposition of A)
Just some fun.
Getting started with scientific programming.
For an individual who has no previous coding experience, playing with Python is the most efficient way to begin in scientific programming. Even very advanced C++/Fortran coders who know Python will confess it’s virtually always the fastest route to small programs and the fastest route to results for “easy-to-medium” tasks. It requires much less “legacy” knowledge (UNIX shell, build systems, debuggers, libraries etc.) than a systems programming language, and it has a very mature open-source suite of scientific libraries basically exceeding the utility of Matlab.
So go ahead and install Python and Scipy/Numpy on your computer. Make some plots with matplotlib. Calculate some eigenspectra. For further reading check out Dive into Python. There’s even whole electronic structure codes wholly realized in Python. Recoding some Numerical Recipes in Python is a worthwhile exercise for anyone who wants to do scientific programming.
In my experience most computational groups do a bad job of sharing code and collaborating on code. At the end of the day this leads to time-wasted due to reduplicated effort, and time wasted trying to find “the version that worked.”. We will use the free tools Bitbucket, and git to share and maintain codes our group works on. There’s a quite nice free book available about git you can easily digest in a weekend.
Reading to get started…
Good books to grab if you want to study electronic structure theory:
The obvious one is Szabo & Ostlund (~7$ on ‘zon) although it’s nowadays quite antiquated.
If you can instead find Helgaker & Jorgenson’s book, I would read it instead.
To learn about Density Functional Theory, Burke’s free manifesto is good.
Of course electronic structure is just a drop in the bucket of science, and I have found these other books quite illuminating:
Tuckerman’s Stat. Mech
Tannor’s quantum dynamics textbook
Nitzan’s book about Condensed Phase Chemical Dynamics
Quantum Many-Body textbook of Fetter and Walecka (a cheap dover gem)
You won’t meet many students who have a mastery of all-of-the above textbooks, but each is very useful for it’s own reasons.
Good papers for all young theoretical chemists to read:
This is a by-no-means exhaustive, subjective list of seminal papers in the area of theoretical chemistry that I will add to slowly. Reading these papers is useful both for the subject of the paper, but also to see how genuinely transformational science is done. To students with a good background this list may seem silly, but to students just beginning it could be quite useful.
General:
Metropolis: http://jcp.aip.org/resource/1/jcpsa6/v21/i6/p1087_s1
Transition state theory: http://jcp.aip.org/resource/1/jcpsa6/v3/i2/p107_s1
Path-Integral:
Parinello & Rahman: http://jcp.aip.org/resource/1/jcpsa6/v80/i2/p860_s1
AIMD:
CPMD: http://link.aps.org/doi/10.1103/PhysRevLett.55.2471
Tully: http://jcp.aip.org/resource/1/jcpsa6/v101/i6/p4657_s1
Quantum Many-Body Problem:
The Failure of PT: http://link.springer.com/article/10.1007%2FBF00698753?LI=true
Coupled-Cluster: http://pra.aps.org/abstract/PRA/v5/i1/p50_1
DMRG: http://prl.aps.org/abstract/PRL/v69/i19/p2863_1
DFT:
Kohn-Sham: http://prola.aps.org/abstract/PR/v140/i4A/pA1133_1
Becke’s functional ingredients: http://link.aps.org/doi/10.1103/PhysRevA.38.3098
and: http://jcp.aip.org/resource/1/jcpsa6/v98/i7/p5648_s1
The group evolving into being…
Hello world!
As of July 2013, we will be a research group modeling chemistry with quantum models of electronic properties at the University of Notre Dame.