Author: Medieval Studies Research Blog

Posted on

Why Fortify?  A Short Introduction to Four Byzantine Fortifications in the Maeander Valley

I chose these four fortresses as representations of the observable differences between Byzantine fortified sites.  Not all fortifications were made equal.  Differences lie not only in the choice of how walls and towers are constructed, but also in the placement of these fortified sites in the landscape.  Careful analysis of these features can reveal the underlying assumptions and motivations of the builders.  I have chosen among these four fortifications a military base, a refuge, a center for agricultural exploitation, and a fortified residence within the Maeander River valley.

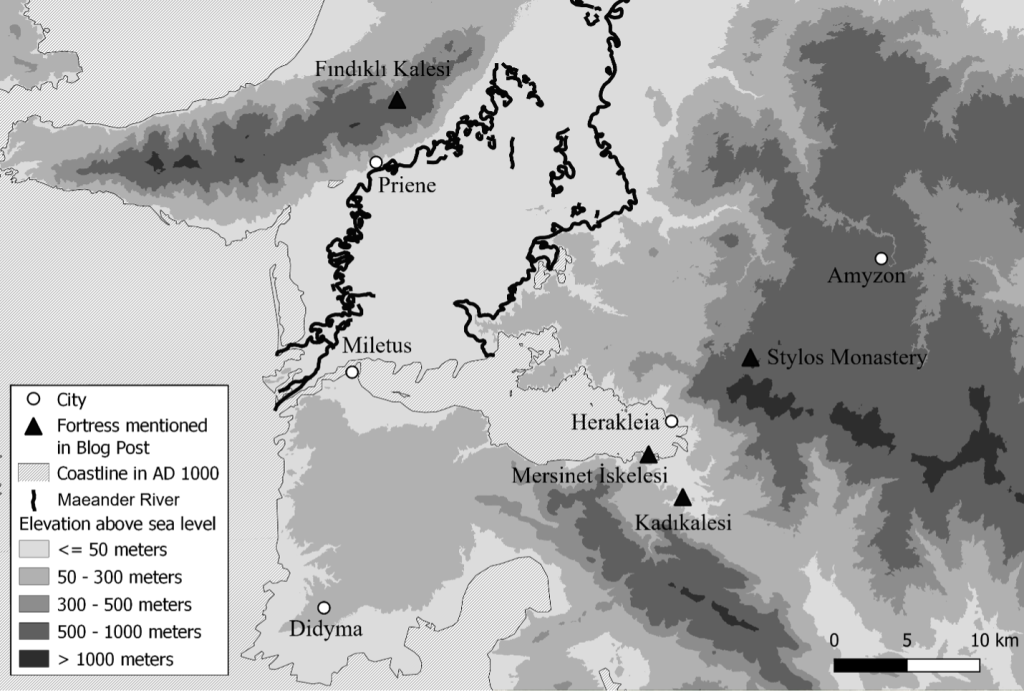
The Locations of the Fortresses, made by author in QGIS.

Kadıkalesi[1]

Kadıkalesi is a great example of a military fortress likely built and used by the Byzantine armed forces.  The entrances, not just the main one but the two postern entrances too, had a bent gate, which denies an attacker a good view inside the fortress (see Figure 2).  The towers project from the walls and include a larger circular tower which is more resilient to projectiles than a square tower.  Throughout the entire circuit of walls, platforms known as battlements were built for soldiers to be able to view the landscape.  The walls were caped with crenulations, which provided coverage for those soldiers from fire from below (see Figure 3).  This fortress was found on a small hill above a road, about 50 meters above sea level.  On the one hand, this elevation gave the soldiers good visibility of the surrounding countryside, but, on the other, it was low enough that the soldiers could quickly do something about a threat (see Figure 2). 

The Bent Gate of Kadıkalesi, photo by author.
The Battlements of Kadıkalesi, photo by author.

Fındıklı Kalesi[2]

Fındıklı Kalesi was a large fortress on the top of a mountain, enclosing an area of seven hectares at an elevation higher than 600 meters above sea level.  Like Kadıkalesi, the walls were built with military concerns in mind; a series of towers and periodic battlements defend the portions of wall spanning the gaps between rocks, while a double gate fortifies the most vulnerable part of the fortress in the southeast.  The size of the fortress was partly determined by geology; the walls follow the edges of a massive rock outcropping.  Unlike Kadıkalesi, however, the fortress was isolated from the Byzantine roads that cross the mountain and unable to serve in the policing of routes.  I agree with scholars who see Fındıklı Kalesi as a refuge for times of invasion with only a small permanent peacetime population.[3]  This was a fortress, not of lords or soldiers, but of farmers and shepherds, who needed its great size to house flocks of sheep and its isolated location to keep just far enough away from any potential raiders that this ‘bluff in stone’ may appear like a formidable military fortress. 

View North from Inside Fındıklı Kalesi, photo by author.

Mersinet İskelesi[4]

The impressive fortress found on the southern coast of Lake Bafa appears to be a military fort like Kadıkalesi.  The use of blind arches to support the battlements even shows an improvement over the thick walls of Kadıkalesi.  However, I argue that military effectiveness was not the main concern of this fortress.  The defining element of the fortress is a great tower bisected by the enceinte wall.  However, there is no communication between the walls and the tower; anyone stationed in the tower could not advance into the battlements in response to a threat.  Second, the tower does not protrude from the wall, which decreased its visibility and potential range of fire.  While Mersinet İskelesi’s position does provide a good view of the eastern half of Lake Bafa, nearby hills could provide a better view.  Instead, this fortress has more in common with the isolated towers found around Lake Bafa and in the wider Maeander Valley.  Mersinet İskelesi is an isolated tower with an increased budget.  I suspect that this fortress and the other towers have something to do with the exploitation of agricultural estates as these towers lie at the edge of the most plentiful area of farmable land adjacent to Lake Bafa, even if this fortress is usually interpreted as a fortified monastery[5] or military base.[6] 

View of Tower of Mersinet İskelesi from Lake Bafa, photo by author.
Central Tower of Mersinet İskelesi from inside the Fortress, photo by author.

The Monastery of Stylos[7]

The final fortress is the monastery of Stylos.  Its walls aided the defense of a community which resided in isolated places like a type of fortified residence.  However, this monastery was never intended to operate like a military fortress.  For instance, the battlements were limited to walls located at known entrances on the north and south side.  They were only interested in watching visitors who intended to use a proper gate and not in observing the wider region.  Nor was it a refuge.  While the monastery was deep in its mountain like Fındıklı Kalesi, Stylos is near a branch of an ancient road network, which gives the monastery a greater ability to interact with others on and off the mountain.  Finally, the division of interior fortification betrays a uniquely monastic concern: the proper veneration of the founder of the monastery.  The inner bastion of the monastery contains the hermitage of Saint Paul the Younger cut in a tower of rock and decorated with a painted program of religious images (see Figures 6 and 7).  I suspect the fortification of the hermitage likely served to encourage the veneration of their founder and to connect that founder with the builder of the walls, likely Christodoulos of Latros who would go on to found the Monastery of Saint John the Theologian on Patmos.  Whatever the purpose of the inner gate was, it is hard to imagine it served the defense of the monastery. 

The Inner Gate of Stylos Leading to the Hermitage, photo by author.
View of the Hermitage of Saint Paul the Younger, photo by author.

Tyler Wolford, PhD
Byzantine Studies Postdoctoral Fellowship
Medieval Institute
University of Notre Dame

[1] Wolfgang Müller-Wiener, “Mittelalterliche Befestigungen im südlichen Jonien,” IstMitt 11 (1961): 19-23.

[2] Hans Lohmann et al., Survey in der Mykale 1, Bonn: Rudolf Habelt, 2014-2017, II.510-513 (MYK 65).

[3] Jesko Fildhuth, Das byzantinische Priene, Berlin: DAI, 2017, 96-98; for an opposing view see Lohmann et al., Survey in der Mykale, I.284-290.

[4] Müller-Wiener, “Mittelalterliche Befestigungen,” 17-19.

[5] Urs Peschlow, “Latmos,” Reallexikon zur byzantinischen Kunst 5 (1995): 695-696.  

[6] Müller-Wiener, “Mittelalterliche Befestigungen,” 18-19.

[7] Theodor Wiegand, Der Latmos, Milet III.1, Berlin: Georg Reimer, 1913, 61-72.

Posted on

Notaries in Medieval and Early Modern Ireland

In June of 2023, I arranged to meet my friend and fellow historian Caoimhe Whelan for a short breakfast during one of my rare trips to Ireland. I had given the rest of the day over to research, a concession of one day in what was supposed to be a family holiday. At breakfast, Caoimhe introduced me to Stuart Kinsella, Christ Church Cathedral’s Research Advisor; he was chasing down the scribes and notaries of the Cathedral’s later medieval manuscripts, and had run across a few pages at the back of my dissertation – an appendix cataloguing all of the notaries I had found in the process of investigating the life and career of Anglo-Irish author and notary James Yonge. In introducing me to Stuart, Caoimhe inadvertently cancelled my vacation. Breakfast was consumed. We talked. We ordered coffee. Stuart got out his carefully compiled list of notaries. We talked some more. Soon we were ordering lunch. We compared images, debated the merits of early 20th-century drawings of documents lost in a catastrophic 1922 fire a half mile from where we sat, and began making plans. By the end of the morning, we had explored several possibilities for a project far wider than my study of James Yonge or Stuart’s study of Christ Church scribes and notaries. Every spare moment I could get for the rest of my time in Ireland was given over to notaries. (Caoimhe would go on to destroy my summer holidays the following year with a grainy image of a notarial signum taken at Sarah Graham’s lecture at Leeds, but that is a tale for another time.)

            Notaries were specialized legal scribes used principally by the ecclesiastical courts to record proceedings and produce official documents. Notaries could be found in every corner of medieval and early modern Europe, and were particularly prevalent on the Italian and Iberian peninsulas where they also played a role in civil courts. In England and English-controlled Ireland, English civil law did not provide for notaries, and as a result they were far fewer in number. Notaries found their way, however, into civil procedures, particularly in cases where an official witness was needed. Notaries not associated with the church were paid by laypeople to produce documents that might be helpful in future cases in the ecclesiastical courts, particularly those regarding marriage or legitimacy.[1] In Anglo-Ireland, these specialized scribes also created new, authenticated copies of documents that had become faded or damaged. Notaries also served as official witnesses in disputes, creating documents functioning similarly to a sworn deposition; their instruments record in a matter-of-fact way dramatic moments in the lives of ordinary people. For instance, a 1406 instrument of James Yonge records that Robert Burnell wanted John Lytill to place his seal on some documents; Lytill refused, and Burnell responded by seizing Lytill in a Dublin street and holding him hostage until he acquiesced.[2] Another instrument by Thomas Baghill records an attempt to interfere in a will. On his deathbed, William Moenes was approached by his brother, Robert, who attempted to claim William’s property, despite the objections of William himself, who even in his extremity protested that he wished his property to go to his uncle’s daughters.[3] Both of these instruments were probably intended for later use in civil cases regarding the disposition of property.

            Notarial instruments are most easily identified by their signa. Each notary developed his own unique signum manuale, a pen-and-ink drawing that he used to authenticate the documents he created. These frequently looked like altar crosses. During the Tudor period, notarial signa became panels of knotwork.

Signum manuale of William Walch (fl. 1525-1538) on a document created in 1525 in the Waterford area and now housed at the National Library of Ireland, D.2129. Image courtesy of the National Library of Ireland.

Once developed, a notary’s signum remained fixed; he would use the same signum for the rest of his career. On an instrument, the signum manuale is also accompanied by an eschatocol, a formulaic attestation that the notary has heard and witnessed what is recorded in the document and that the contents are true to the best of the notary’s knowledge. Eschatocols frequently begin with an E that can be quite plain or highly ornamented, depending on the notary. Again, notaries’ Es tended to remain somewhat fixed. The signum and eschatocol provide a key to identifying a notary’s handwriting in other contexts. For instance, James Yonge was also the scribe of over one hundred surviving documents, signed and unsigned. Notary William Somerwell, who worked for the archbishops of Armagh, was also one of the principal contributors to the registers of archbishops Nicholas Fleming (1404-1416), John Swayne (1418-1439), John Prene (1449-1453), and John Mey (1443-1456).

Signum manuale of William Somerwell (fl.1422-1459), on a document bound into the Registrum Iohannis Mey, PRONI DIO 4/2/6, Book 3, fol. 393, reproduced by permission of the Deputy Keeper of Records, Public Record Office of Northern Ireland (PRONI).

Signa have also been instrumental in identifying groups of notaries. For instance, James Yonge’s student Thomas Baghill borrowed portions of his master’s signum when developing his own.[4]

Signum manuale of James Yonge (fl. 1404-1438), deeds of the Guild of St. Anne, Royal Irish Academy 12.S.22–31, no. 343 (12 December 1432). By permission of the Royal Irish Academy © RIA.
Signum manuale of Thomas Baghill (fl.1419-1439). Note Baghill’s imitation of Yonge’s cross outline. Deeds of the Guild of St. Anne, Royal Irish Academy 12.S.22-31, no. 253 (27 January 1431). By permission of the Royal Irish Academy © RIA.

We’ve also discovered signa in contexts outside of notarial instruments. Of particular note is the signum of an as-yet-unidentified notary in the margins of a Hiberno English translation of Gerald of Wales’ Expugnatio Hibernica.[5]

Our survey of Anglo-Irish notaries is still in its infancy, and we are seeking sources of funding. We are currently trying to document as many notaries from medieval and early modern Ireland as possible as an entry into a larger exploration of notaries’ training, scribal networks, and documents. We hope to create a searchable online database of notarial marks and scribal hands for Ireland as a starting point for a more extensive resource cataloging the marks of medieval and early modern notaries of the British Isles. We would also love to see a future collaborative database of European notaries.

            Ian Doyle once wrote of palaeography that “the jigsaw puzzle we are all working on is so big that it may need the help of every eye to try to fit a piece in it.”[6] We believe the same is true of medieval and early modern notaries. This is where you, dear reader, come in. We heartily invite researchers in any area of medieval and early modern Europe to let us know about any notaries or notarial signa you encounter in your own research. The project’s email address is notarius.ie@gmail.com. We welcome your comments and contributions!

Theresa O’Byrne

Associate Researcher, Virtual Record Treasury of Ireland

Latin and history instructor, Delbarton School

[1] C.R. Cheney, Notaries Public in England in the Thirteenth and Fourteenth Centuries. Oxford: Clarendon Press, 1972, p. 56; Patrick Zutshi, “Notaries Public in England in the Fourteenth and Fifteenth Centuries,” Historia, Instituciones, Documentos 23 (1996), pp. 421-33, at p. 426.

[2] Trinity College Dublin MS 1477, no. 69, 16 March 1406.

[3] Royal Irish Academy 12.S.22-31, no. 826, 17 April 1434.

[4] Theresa O’Byrne, “Notarial Signs and Scribal Training in the Fifteenth Century: The Case of James Yonge and Thomas Baghill,” Journal of the Early Book Society 15 (2012): 305–18.

[5] Trinity College Dublin MS 592, fol. 6v.

[6] A.I. Doyle, ‘Retrospect and Prospect’, in Manuscripts and Readers in Fifteenth-Century England, ed. D. Pearsall (Cambridge, 1983), pp. 142–6 (pp. 145–6).

Posted on

Mathematical “Small Things” and the Quadrivium

What did early mathematical education look like in the Middle Ages? As is commonly known, the ideal Liberal Arts curriculum of the Middle Ages featured both the Trivium (dedicated to the study of words) and Quadrivium (dedicated to the study of nature in the form of mathematical arts). The Trivium included Grammar, Logic, and Rhetoric. The Quadrivium consisted of Music, Astronomy, Geometry, and Arithmetic. These seven ways (viae) of liberal arts learning prepared students who studied them diligently to “comprehend everything that they read, elevat[ing] their understanding to all things and empower[ing] them to cut through the knots of all problems possible of solution” (John of Salisbury, Metalogicon I.12). Even today, the concept of a Liberal Arts education that prepares a student for life and whatever (foreseen and unforeseen) challenges lay aheadremains. And yet, for anyone who has educated a child, the idea of delaying mathematical education until the early teen years (which is when the formal Quadrivium was taught) seems completely impractical and misguided.

Unknown Miniaturist, French (active 1190s Paris). Bodleian Library, MS Laud Misc. 409 (Oxford Manuscript ) f.3v.

Did medieval educators really wait until students had a full understanding of the Trivium before introducing mathematics? The difficulty here comes in part from the lack of extensive knowledge of the curriculum of early childhood medieval education, including mathematical instruction. The institutions for learning changed over time and even geographic region. Early childhood education could take place in a home, in a monastery, or at a local cathedral school. Another difficulty may also be that our cultures mean slightly different things when we talk about the discipline of mathematics.

The “paper trail” for exactly what early childhood mathematical education might have looked like is not vast. But one tiny, but vivid, glimpse of what boyhood mathematical pursuits might have looked like can be seen in the writings of Hugh of St. Victor, an early twelfth century canon regular who wrote a book on the Liberal Arts called the Didascalicon. In this work, Hugh of St. Victor gives a rare view of his own early mathematical education:

I laid out pebbles for numbers, and I marked the pavement with black coals and by a model placed right before my eyes, I plainly showed what difference there is between an obtuse-angled, and an acute triangle. Whether or not an equilateral parallelogram would yield the same area as a square when two of its sides were multiplied together, I learned by walking both figures and measuring them with my feet. Often I kept watch outdoors through the winter nights like one of the fixed stars by which we measure time. Often I used to bring out my strings, stretched to their number on the wooden frame, both that I might note wih my ear the difference among the tones and that I might at the same time delight my soul with the sweetness of the sound. These were boyish pursuits…yet not without their utility for me, nor does my present knowledge of them lie heavy upon my stomach. (VI.3)

Hugh describes these activities as grounding him “in things small” so that he could “safely strive for all” later in life.

Notice how many of the activities mentioned by Hugh of St. Victor do not require a textbook at all, especially with a charismatic teacher, or in the case of Hugh’s own life, a particularly inquisitive child. Counting and the study of angles required only pebbles. The figuring of surface area required only the measurement of feet. An early acquaintance with the stars required actually going out to look at the night sky, even when it was cold, and the study of the relationship between musical notes came from literally fiddling around with a simple stringed instrument. To these activities, we might presumably add the common medieval practices of singing (cantus) and possibly dancing in set patterns. Or the calculating of times and seasons (computus). Or measurements of land and sea masses for commerce or geography. Or ratios for cooking. Many of these activities can be conveyed orally through constant interaction with numbers in the physical world. That is not to say that no formal study or book learning could or was be done in these areas, but the bulk of early mathematical learning did not need to take place in a school environment with a textbook. All that was needed was a student, the physical world, and a teacher with mathematical knowledge.

Christine and the Sybil pointing to a ladder from the heavens, from the Book of the Queen, France (Paris), c. 1410-1414, Harley MS 4431, f. 189v.

What Hugh recognized was that these mathematical activities, whether for play or practical application, were essential for what he and his contemporaries would have considered the formal discipline of mathematics as a liberal art (i.e. the Quadrivium), which would have taken place during the teenage years at higher level schools. Hugh distinguishes arts and disciplines in the following manner: “Knowledge can be called an art ‘when it comprises the rules and precepts of an art’ as it does in the study of how to write; knowledge can be called a discipline when it is said to be ‘full’ as it is in the ‘instructional’ science, or mathematics” (II.1).

A table used for Computus. Harley MS 3667 f 001v.

 In other words, the sorts of activities Hugh describes himself doing as a boy were not mathematical disciplines in his terminology. Instead, his boyish mathematical play was both pleasant at the time and useful as he grew up to study the mathematical disciplines. For this reason, Hugh praised such activity as best because it aids one’s movement “step by step” rather than “fall[ing] head over heels when [attempting] to make a great leap ahead” (VI.2). This learning process mirrors the original discovery of the disciplines themselves by humanity. As Hugh writes:

Such was the origin of all the arts; scanning them all, we find this true. Before there was grammar, men both wrote and spoke; before there was dialectic, they distinguished the true from the false by reasoning; before there was rhetoric, they discoursed upon civil laws; before there was arithmetic, there was knowledge of counting; before there was an art of music, they sang; before there was geometry, they measured fields; before there was astronomy, they marked off periods of time from the courses of the stars. But then came the arts, which, though they took their rise in usage, nonetheless excel it. (I.11)

Early childish mathematical play was not the Quadrivium, but Hugh considered it a necessary preparation for the later study of the Quadrivial arts. Just as Boethius argued in Institutio arithmetica 1,1,7 that the quadrivium provides steps (gradus) by which the mind is progressively illuminated and can raise itself from its immediate sensible circumstances to the certainty of intelligible truth, so Hugh argued that the humble mathematical play of childhood was one step on the way to learning the discipline of mathematics. Computus, stargazing, learning to sing, learning to dance, and making geometric shapes with pebbles—none of this was Quadrivium. These activities could be boyhood pursuits…or in some cases, ends in themselves practiced into adulthood, but activities of this sort were, in Hugh’s opinion, a necessary preparatory step for the Quadrivial disciplines.

Lesley-Anne Dyer Williams
Public Humanities Postdoctoral Fellow
Medieval Institute
University of Notre Dame

Lesley-Anne Dyer Williams is a Professor for Memoria College’s Masters of Arts in Great Books program and graduated with her doctorate from the University of Notre Dame’s Medieval Institute in 2012. She was also the founding director Liberal Arts Guild at LeTourneau University. Her research focuses upon twelfth-century Platonism and poetry, especially Thierry of Chartres and Bernard Silvestris.

Further Reading:

Hugh of St. Victor. The Didascalicon of Hugh of St. Victor:  A Medieval Guide to the Arts. Edited & translated by Jerome Taylor, Columbia University Press, 1991.

Jaeger, C. Stephen. The Envy of Angels: Cathedral Schools and Social Ideals in Medieval Europe, 950-1200. University of Pennsylvania Press, 1994.

John of Salisbury. Metalogicon. Translated by C.C.J. Webb, Clarendon Press, 1929.

Orme, Nicholas. Medieval Children. Yale University Press, 2001.

Orme, Nicholas. Medieval Schools. Yale University Press, 2006.