Plato – Medieval Studies Research Blog: Meet us at the Crossroads of Everything

June 5, 2024June 13, 2024

Plato, Mathematician and Myth-Maker

Pisano, Giovanni, 1240?-1320?. c.1284. Siena Duomo: det.: Plato. Place: Museo dell’Opera del Duomo (Siena, Italy). https://library-artstor-org.proxy.library.nd.edu/asset/ARTSTOR_103_41822000532257.

The Republic, The Symposium, The Phaedrus, The Apology, and The Phaedo––these are just a few of the works of Plato that were not widely available throughout most of the Middle Ages. No extended depiction of the most just city in the Republic. No discussion of love in The Symposium and The Phaedrus. No self-defense for Socrates at his trial as found in The Apology, and no final dialogue before his suicide as found in The Phaedo. For lovers of great texts, especially Plato, such news can be shocking. What kind of Plato does a person know if they don’t have these key works? How much of Socrates’ life and Plato’s philosophy could even be known? These are the questions that many medieval scholars of the Latin Platonist tradition have dedicated their lives and careers to answering, and the answers can be quite surprising.

One aspect of this research that ought to be appreciated by the wider reading public (outside of the narrow confines of medievalists) is that Plato’s Timaeus wasthe most widely available Platonic work throughout most of the Middle Ages. In fact, examining the text of the Timaeus and why itwas such one of the few Platonic texts preserved reveals how peculiarly modern our current canon of Platonic literature is.

What we value in Plato was not necessarily what late antique or medieval readers valued, and yet, their ability to read well meant that they understood a lot more than might be supposed. An attention to the reception history of Plato’s Timaeus can give modern readers of Plato a better appreciation for the importance of both mathematics and poetry in Platonic philosophy.

The Timaeus is Plato’s work on the origins of the universe. It begins with a dialogue between Timaeus, Socrates, Hermocrates, and Critias, in which Socrates expresses a desire for a “moving image” of the city they had been talking about the day before. The summary of the previous day’s discussion appears to bear some resemblance to the conversation found in the Republic although scholars are divided over whether this summary perfectly matches the Republic that we now possess. Regardless of its accuracy, this summary would have been the closest a medieval reader would have had to a taste of the Republic. The opening dialogue covers all sorts of fascinating topics from Solon’s visit to Egypt, oral culture, the mythic origins of writing, and the myth of Atlantis, but the bulk of the work features a narration about the origins of the universe recounted by the Pythagorean, Timaeus.

The Timaeus was received in the Middle Ages through three main channels of Latin translations: the translation of Calcidius (which ends at 53b), the translation of Cicero (available but not widely used or even known, which ends at 42b), and the excerpts from the Ciceronian translation of the Timaeus that can be found in Augustine’s City of God. Although it does not contain the whole text of the Timaeus, Calcidius’ translation is much more complete than Cicero’s: rather than giving merely the speech of Timaeus like Cicero’s translation does, it includes the opening dialogue (even though the commentary itself ignores it).

Most modern Plato scholars would probably not choose The Timaeus as theone and only work they could save from destruction for all time. But, a better understanding of who Calcidius was and why he wrote the commentary on the Timaeus suggests that the preservation of the Timaeus in the Latin West was not an accident of fate. Rather, the results of Gretchen Reydams-Schills’ lifelong study of Calcidius give a plausible reason for why Calcidius’ commentary may have been the Platonic work of choice for many late antique philosophers.

Reydams-Schils argues that Calcidius wrote his commentary as an introduction to the Platonic corpus, essentially reversing the Middle Platonic curriculum, which traditionally ended with the Timaeus. One major piece of evidence for this theory is that Calcidius’ commentary often reserves discussion of harder philosophical concepts for the end of the commentary.Furthermore, unlike the Neoplatonists, Calcidius did not read the Timaeus synoptically and believed strongly in the importance of sequential reading of the Platonic corpus. In Calcidus’ Platonic curriculum, the Timaeus came first with its teachings on natural justice, then the Republic with its teaching of positive justice, and finally, the Parmenides came with its teaching of the forms and intelligible realities. Calcidius believed that a thorough understanding of mathematics was necessary for understanding of almost all of the Platonic works, which is why his commentary on the Timaeus turns out to be something like a crash course in Pythagorean mathematics.

Thus, although the Timaeus was one of the only Platonic works available throughout the early Middle Ages, Calcidius’ commentary gave readers some introduction to the entire Platonic corpus as well as a great deal of Pythagorean mathematics. Perhaps there might be good reason for a philosopher to save The Timaeus (especially a copy with Calcidius’ commentary)from a burning building!

Plato; Chalcidius (translation). *Timaeus.* Manuscript. Place: Bodleian Library, University of Oxford, <a href=’http://www.bodley.ox.ac.uk/’>http://www.bodley.ox.ac.uk/</a>. https://library-artstor-org.proxy.library.nd.edu/asset/BODLEIAN_10310768399.

Medievalists who study the textual reception of the various translations of The Timaeus have been able to identify a shift in kinds of interest in Plato over time. The primary Latin translation of the Timaeus used until the eleventh century was Cicero’s. Medieval scholars used to assume that the revival of Calcidius began with the twelfth century Platonists, but Anna Somfai has demonstrated that the proliferation of copies of Calcidius’ text and commentary began in the eleventh century when championed by Lanfranc of Bec (c.1050). The late twelfth-century actually experienced a decline of copying the Timaeus as interests shifted towards other texts.

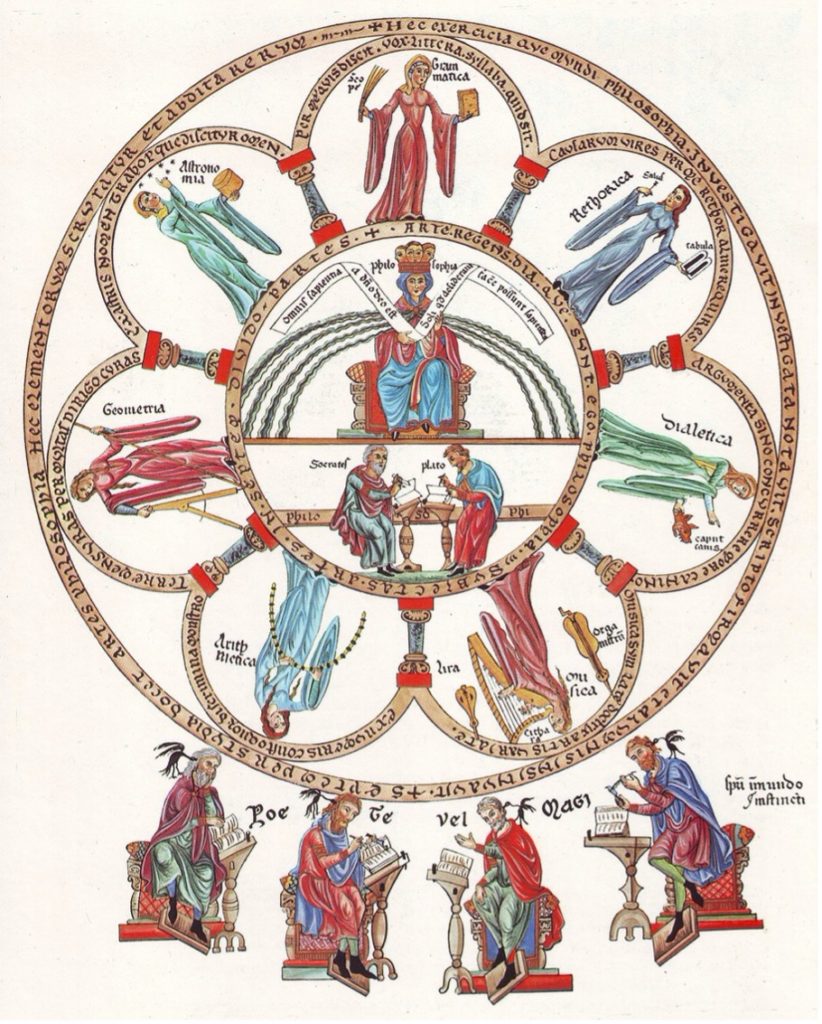
What motivated the eleventh-century interest in Calcidius appears to have been the mathematical content of the Calcidian commentary because, by the Carolingian period, much of the actual content of the quadrivial arts had been lost, and scholars in the Middle Ages attempted to piece together what scraps of it remained from a variety of sources. Calcidius’ commentary on the Timaeus appears to have been particularly valued as a source text for the quadrivial (or mathematical) arts. As my two previous MI blogs have explored here and here, medieval thinkers in the traditional liberal arts tradition recognized that the quadrivial arts were the foundation for philosophical thought, even if they had few textual sources for actually studying them.

And although some of the interest in the kinds of mathematics found in the Timaeus and Calcidius’ commentary may have declined after the twelfth century, it was by no means lost completely. As David Albertson has demonstrated, the mathematical interest in Plato found in the work of the twelfth-century scholar, Thierry of Chartres, would eventually be picked up by the fifteenth-century scholar, Nicholas of Cusa, and many scholars have noted resonances of Cusa’s quadrivial agenda in the thinking of Leibniz, the founder of calculus:

It seems that God, when he bestowed these two sciences [arithmetic and algebra] on humankind, wanted to warn us that a much greater secret lay hidden in our intellect, of which these were but shadows. (Leibniz as quoted by Albertson, p.2)

Bernardus Silvester. *Liber fortunae*, also known as *Experimentarius*.. Manuscript. Place: Bodleian Library, University of Oxford, <a href=’http://www.bodley.ox.ac.uk/’>http://www.bodley.ox.ac.uk/</a>. https://library-artstor-org.proxy.library.nd.edu/asset/BODLEIAN_10310765350.

Even though the interest in scribal copying of the Timaeus seems to have declined somewhat by the twelfth-century, another kind of imitatio or translatio studii was being enacted by a different kind of scholar, Bernard Silvestris. He wrote a prosi-metric telling of the creation of the world that emulates Plato’s Timaeus. The title of his work, Cosmographia, roughly translates as “universe writing,” and Bernard delivered an oral performance of itbefore Pope Eugenius III in 1147. Bernard’s creative retelling of the Timaeus poetically depicts the role of imitation in the divine creation of the world in the form of “divine writing.” Performatively, the Cosmographia demonstrates that this divine writing is then imitated by poets in the form of human writing. In other words, Bernard values Plato’s Timaeus here not merely for its insights into mathematics or even the structure of the universe, but also what this mathematics in the universe implies about the mimetic nature of poetry itself.

As many literary scholars have demonstrated, much of the European literary tradition follows suit in seeing the value of Timaean Platonism for the production of literature. This interest can be seen in such diverse authors as Alan of Lille, Chrétien de Troyes, and Dante.

While I would personally be loath to give up the access to the Platonic corpus that I possess, the medieval reception of the Timaeus constantly pushes me to reconsider how I am reading that corpus. Having a large corpus of texts actually places an onus on the modern reader to ask the question of where to place the textual emphasis: Which texts of Plato should be considered central (and which ones periphery) and why? For example, should Plato’s Republic be considered his last word on poets and poetry? What would happen if Plato’s Timaeus were given more weight?

C.S. Lewis once wrote in his introduction to On the Incarnation by Athanasius:

Every age has its own outlook. It is specially good at seeing certain truths and specially liable to make certain mistakes. We all, therefore, need the books that will correct the characteristic mistakes of our own period. And that means the old books.

These words about reading the great books can also apply to reading the old books as they were read by past readers. Understanding medieval readings of Plato might very well be a good counterweight to modern presuppositions about who Plato was and what he was about. How might the idea of Plato as both a mathematician and myth-maker transform our modern understanding of Platonism and its history?

Lesley-Anne Dyer Williams is a Professor for Memoria College’s Masters of Arts in Great Books program and graduated with her doctorate from the University of Notre Dame’s Medieval Institute in 2012. She was also the founding director Liberal Arts Guild at LeTourneau University. Her research focuses upon twelfth-century Platonism and poetry, especially Thierry of Chartres and Bernard Silvestris.

Lesley-Anne Dyer Williams
Public Humanities Postdoctoral Fellow
Medieval Institute
University of Notre Dame

For Further Reading:

Albertson, David. Mathematical Theologies: Nicholas of Cusa and the Legacy of Thierry of Chartres. Oxford University Press, 2014.

Baxter, Jason M. The Infinite Beauty of the World: Dante’s Encyclopedia and the Names of God. Peter Lang, 2020.

Bernardus Silvestris. Poetic Works. Edited by Winthrop Wetherbee, vol. 38, Harvard University Press, 2015.

Caiazzo, Irene. “Teaching the Quadrivium in the Twelfth-Century Schools.” A Companion to Twelfth-Century Schools, edited by Cédric Giraud, translated by Ignacio Duran, vol. 88, Brill, 2019, pp. 180–202.

Calcidius. On Plato’s Timaeus. Edited by John Magee, vol. 41, Harvard University Press, 2016.

Chenu, M. D. “The Platonisms of the Twelfth Century.” Nature, Man and Society in the Twelfth Century: Essays on New Theological Perspectives in the Latin West, translated by Jerome Taylor and Lester K. Little, vol. 37, University of Toronto Press, 1997.

Dronke, Peter. The Spell of Calcidius: Platonic Concepts and Images in the Medieval West. SISMEL edizioni del Galluzzo, 2008.

Gersh, Stephen. Middle Platonism and Neoplatonism: The Latin Tradition. Vol 1 and Vol 2. University of Notre Dame Press, 1986.

Hoenig, Christina. Plato’s Timaeus and the Latin Tradition. Cambridge University Press, 2018.

Murray, K. Sarah-Jane. From Plato to Lancelot. Syracuse University Press, 2008.

Plato. Plato’s Cosmology: The Timaeus of Plato Translated with Running Commentary. Edited by F. M Cornford, Routledge, 1937.

Reydam-Schils, Gretchen. “Myth and Poetry in the Timaeus.” Plato and the Poets, edited by Pierre Destrée and Fritz-Gregor Herrmann, Brill, 2011.

Reydams-Schils, Gretchen J. Calcidius on Plato’s Timaeus: Greek Philosophy, Latin Reception, and Christian Contexts. Cambridge University Press, 2020.

Somfai, Anna. “The Eleventh-Century Shift in the Reception of Plato’s Timaeus and Calcidius’ Commentary.” Journal of the Warburg and Courtauld Institutes, vol. 65, 2002, pp. 1–21.

Stock, Brian. Myth and Science in the Twelfth Century. Princeton University Press, 1972.

Wetherbee, Winthrop. Platonism and Poetry in the Twelfth Century. Princeton University Press, 1972.

January 31, 2024February 9, 2024

Poetry as a Quadrivial Art?

“That ‘Poetry is the cradle of philosophy’ is axiomatic”
(John of Salisbury, Metalogicon I.22).

Coëtivy Master (Henri de Vulcop?) (French, active about 1450 – 1485), *Philosophy Presenting the Seven Liberal Arts to Boethius*, Google Art Project.

It is a truth generally acknowledged that in the Middle Ages a liberal arts education consisted of the trivium (grammar, logic, and rhetoric) and the quadrivium (arithmetic, music, geometry, astronomy). Poetry –what we might call “literature”– was primarily taught by grammarians and rhetoricians in the Middle Ages. Literary scholars, like Rita Copeland and Marjorie Woods, have therefore been very motivated to study exactly what the language disciplines of Grammar and Rhetoric entailed and precisely how they were taught in order to have a better sense of what the study of literature must have looked like in this period. Their works are indispensable for the study of medieval literature and truly are the bulk of where instruction in poetics lay in the Middle Ages. And yet, once cannot stop there.

Knowing exactly where to put poetry was something that clearly bothered many medieval philosophers. While today we might assume that poetry would clearly be associated with the Trivium, or the arts dedicated to words, specifically grammar and rhetoric, certain medieval thinkers located it within logic and also the Quadrivium, or the arts of number. Understanding why can help us to understand the multi-faceted way in which the medieval mind approached poetry in particular and the literary arts more generally.

Étienne Colaud, “John of Salisbury teaching philosophy,” frontispiece miniature of the *Policraticus* by John of Salisbury, BnF Ms.1145, folio 3 recto, Public domain, via Wikimedia Commons.

In the twelfth century when there were major curricular changes afoot in schools and universities, John of Salisbury maintained that poetry belonged to the art of grammar although it was closely allied with rhetoric. “Art,” writes John of Salisbury, “is a system that reason has devised in order to expedite, by its own short cut, our ability to do things within our natural capacities. Reason neither provides nor professes to provide the accomplishment of the impossible;” Instead, reason pursues the possible by means of an efficient plan, what the Greeks would call a methodon (Metalogicon I.11, p.33). As J.J. Murphy writes in the Cambridge History of Literary Criticism, Vol. II: The Middle Ages:

In medieval terminology the Latin word ars (plural: artes) denoted a body of principles relating to a specific activity such as painting, music, preaching, or writing. By extension the term was also used for a written treatise on the subject of a particular art […] The term ‘art’ or ars when applied to such a treatise indicates a discussion of what the ancient Greeks would have called techné ––‘technique’ or ‘craft’ –– rather than an abstract or theoretical discussion of a subject (p.42).

The practitioner of an art is therefore called an artifex or craftsman, and the study of the art consisted of both the intrinsic principles for practice and the extrinsic practice of the art itself.[1] When art is understood in this way, craftsmen generally agree that the person able to produce art is more skilled that the person skilled at conveying the principles underlying art. While poetry was clearly a craft that required a practitioner to study a method of practice, it was by no means clear where it ought to fit in the medieval curriculum of the arts.

John of Salisbury reports that some people thought poetry should be its own subject (shockingly!) because so much of it is clearly a “product of nature’s workshop” (Metalogicon I.18). The close tie between poetry and nature formed the basis of their argument, but John of Salisbury warns pragmatically that if poetry is removed from grammar, “its mother and the nurse of its study,” the study of poetry could be “dropped from the roll of liberal studies.” In other words, everyone studies grammar, which in those days often included a careful study of works like Virgil’s Aeneid. If poetry became its own subject, people might not take it at all!

**English:** Arabic translation of Aristotle’s Poetics by Abu Bishr Matta
**Français :** Poétique (Aristote) en arabe – Abu Bishr Matta
**العربية: فن الشعر لأرسطوطاليس نقل أبي بشر متى – من مخطوطة باريس ٢٣٤٦**
http://gallica.bnf.fr/ark:/12148/btv1b8422956q/f273.image

Some philosophers thought that poetry actually belonged to the subject of logic. These people were especially concerned about how to classify Aristotle’s Poetics. In Ancient Greece, Aristotle had written a group of works (one might even say lecture notes) on logic when teaching at the Lyceum. His followers, the Peripatetics, classified these works as the Organon, meaning instrument or tool, because they saw them as instrumental in preparing for the study of philosophy. The Latin West had only select works from the Organon until their increased contact with Arabic philosophers like Avicenna, who wrote a commentary on the Poetics. Following the Greek commentators on Aristotle, most of the Arabic (and subsequently Latin scholastic) commentators saw Aristotle’s Rhetoric and Poetics as the seventh and eighth works of Aristotle’s Organon. In their zeal, therefore, to comment on the entirety of the Organon, some Latin scholastic commentators, like Herman the German, viewed poetics as a part of Logic.

As surprising as it might be to think that poetry should be considered primarily within the context of “logic,” there is strong evidence that poetry was also studied within the context of the quadrivium. And yet, many medieval thinkers, the Pythagorean believed that number lay at the root of creation itself. For example, Dante writes in the Convivio when commenting on the beauty of a canzone:

All of you who cannot perceive the meaning of this canzone, do not reject it on that account, but consider its beauty: considerable for the way it is constructed, which is the concern of the grammarians; the ordering of its discourse, which is the concern of the rhetoricians; and for the metrical numbering of its parts, which is the concern of poets. (II.xi.9–10)

The key word to focus upon here is numbering. Familiarity with the Commedia and its frequent references to the starsis enough to convince a reader that one aspect of the numbering that Dante had in mind was the medieval discipline of astronomy, but there is also good reason to think that Dante had music in mind. Some of this evidence is textual…the numerous references to music in the Purgatorio and Paradiso…, but some of this evidence can be found in Boethius.

The standard textbook for the teaching of music theory in the Middle Ages was Boethius’ Fundamentals of Music, and until 1255, it was not uncommon for most educated men , including Dante, who undertook a liberal arts education to have at least some instruction in the subject.[2] As a result, even 11^th and 12^th c. philosophers like Anselm and Peter Abelard wrote sacred poetry and song. In this book, Boethius speaks of poetry as a subset of one kind of music.

Boethius begins his work on music with a philosophical justification for its study. Citing Plato and Pythagoras, he observes that music is so deeply engrained in human nature that from a young age it has the power to move human souls, transform their character, and even affect their health and sense of well-being (I.1.180–185). He explains that this phenomenon should leave us with no doubt that “the order of our soul and body seems to be related somehow through those same ratios by which subsequent argument will demonstrate sets of pitches, suitable for melody, are joined together and united” (I.1.186). Since “music is so naturally united with us that we cannot be free from it even if we so desired,” then “the power of the intellect ought to be summoned so that this art, innate through nature, may be mastered, comprehended through knowledge” (I.187). In this way, Boethius justifies the study of music because it reflects something about the fundamental nature of the human soul.

English: “King David, Lady Music and musicians”. In manuscript “De institutione musica”. Boetius.
Español: “El Rey David, la Señora Música y los músicos”. Del manuscrito “De institutione musica”. Boecio.
Date Original: 1941 – 1942. Copy upload: 2010.Source: http://images.amazon.com/images/P/B000009OM1.jpg

In this work, Boethius identifies three kinds of music––cosmic, human, and instrumental. This categorization implies that the human response to music is rooted in the nature of not only the human soul but of the cosmos (I.2). Cosmic music, or the music of the spheres, is the harmonious sound produced when the stars in their courses and the diversity of seasons move swiftly together in harmonious union (1.2.187–188). Human music does not concern the music produced by humans. Rather, it is the music found in the harmony of soul and body in a human being. Boethius describes this music as “a careful tuning of low and high pitches as though producing one consonance” (I.2.189). It unites not only the rational and animal parts of the soul, but the parts of the body and the body’s union with soul. Boethius promises to speak about this subject later, but he never returns to it. Instrumental music, for Boethius, includes the harmonious sounds produced by tension of strengths, human breath, percussion, etc. (I.2.189). This kind of music is what most people today associate with music, but Boethius’ understands this music to operate according to the same mathematical principles of both cosmic and human music. This mathematical concordance explains the reasons for music’s profound effect on the human soul.

Although the producer of cosmic and human music is ultimately God, instrumental music must be produced by a human musician. Boethius’ definition of a human musician broadens the horizon within which music itself is narrowly considered today. He identifies three classes of musician: the instrumentalist, the poet, and the rational judger of music (I.34.224).

The instrumentalist is no greater than a “slave” because one does not need the faculty of reason in order to produce music upon an instrument.

The second class of poets are presumably higher than slaves, but Boethius remarks that even the poets create songs by instinct rather than reason. One might recall here Lady Philosophy’s attack upon the Muses as “harpies” because their base songs only continued to prolong Boethius’ misery.

The third class of musician is the one with the ability to judge rhythm, melody, and composition. Since this class exercises reason in their experience of music, they alone should be considered worthy of esteem. This final judgment may seem harsh, but it was a common opinion in his day; Augustine repeats a similar idea in De musica.³ In fact, both men express their love of hearing music with some guilt, even though Augustine insists that music should remain in churches (Conf. 9.6, 14 and 10, 33, 49–50; Consol. I.2 and IV.6.6). In other words, Boethius repeats the infamous attack of Plato on the poets, even though he himself writes poetry in the Consolatio.

It is startling to consider that Boethius includes both poets and song-writers within the class of musicians. Any time a human being takes the mathematics of sound seriously in the construction of a work of verbal art, they are a musician, whether or not the words constructed are intended for accompaniment with music. Second, Boethius boldy asserts that the ability to judge music is superior to the ability to craft and perform music. Within this model of music, the music theorist and literary critic are both superior to the musician and the poet. The ability to judge is always to be preferred over the ability to craft. In the long war between philosophy and poetry, philosophy always wins.

Whether or not poets like Dante would have agreed with Boethius that the practice of their art was inferior to those who judge art, especially since arts are, by definition, intended to be practiced, it is interesting to consider that medieval poets, as a kind of musician, may have conceived themselves to be craftsman that used the tools of grammar, logic, rhetoric, and music (or the entire quadrivium if one is Boethius or Dante!) to construct their art while looking up at the stars.

Lesley-Anne Dyer Williams
Public Humanities Postdoctoral Fellow
Medieval Institute
University of Notre Dame

Further Reading

Ancius Manlius Severinus Boethius. Fundamentals of Music. Edited by Claude V. Palisca. Translated by Calvin M. Bower. New Haven and London: Yale University Press, 1989.

Copeland, Rita, and Ineke Sluiter. Medieval Grammar and Rhetoric: Language Arts and Literary Theory, AD 300 -1475. Oxford: Oxford University Press, 2009.

Dante Alighieri. Dante: Convivio. Translated by Andrew Frisardi. New edition. Cambridge: Cambridge University Press, 2022.

Fournier, Michael. “Boethius and the Consolation of the Quadrivium.” Medievalia et Humanistica, no. 34 (2008): 1–21.

John of Salisbury. The Metalogicon. Translated by Daniel D McGarry. Berkeley: Calif. U.P., 1962.

Martianus Capella. Martianus Capella and the Seven Liberal Arts. Translated by William Harris Stahl, Richard Johnson, and E.L. Burge. Vol. II: The Marriage of Philology and Mercury. 2 vols. Records of Western Civilization 84. Columbia University Press, 1992.

Minnis, A. J., and A. B Scott, eds. “”Placing the Poetics: Herman the German; An Anonymous Question on the Nature of Poetry.” In Medieval Literary Theory and Criticism c.1100–1375: The Commentary Tradition, Revised. Oxford: OUP, 1991.

O’Daly, Gerard J. P. The Poetry of Boethius. Chapel Hill and London: The University of North Carolina Press, 1991.

Stahl, William Harris, Richard Johnson, and E.L. Burge. Martianus Capella and the Seven Liberal Arts. Vol. I: The Quadrivium of Martianus Capella. 2 vols. Records of Civilization, Sources and Studies 84. New York: Columbia University Press, 1971.

Woods, Marjorie Curry. Classroom Commentaries: Teaching the Poetria Nova across Medieval and Renaissance Europe. 1 edition. Text and Context. Ohio State University Press, 2017.

Woods, Marjorie Curry. Weeping for Dido: The Classics in the Medieval Classroom. 1st ed. Vol. 1. E. H. Gombrich Lecture Series. United States: Princeton University Press, 2019. https://doi.org/10.1515/9780691188744.

[1] Distinctions made by Thierry in the Heptateuchon.

[2] Huglo, “The Study of Ancient Sources of Music Theory in the Medieval University.”

October 4, 2023October 5, 2023

The Quadrivium and the Stakes for Ordering the Mathematical Arts

Fyodor Bronnikov, *Pythagoreans’ Hymn to the Rising Sun*, 1869. Oil on canvas.

Legend has it that Pythagoras sentenced the first person to discover irrational numbers, Hippasus of Metapontum (c.530-450 BC), to death. He was tossed overboard a ship to drown. Why? Pythagoras taught that number was the essence and cause of all things, and for Pythagoras and his followers, numbers meant integers. Hippasus’ discovery of irrational numbers appeared to undermine the very core of Pythagoras’ teachings about the numerical nature of the universe. The secret could not get out. Hippasus had to die.

Imaginary engraving of the philosopher Hippasus of Metapontum. From the 1580 book *Illustrium philosophorum et sapientum effigies ab eorum numistatibus extractae*, by Girolamo Olgiati. Reprinted 1583.

The existence of irrational numbers became a Pythagorean secret. They were called “unutterables” because in Greek, the ratio between two integers was called logos, and so, irrational numbers were called, alogos, which can be translated as either “irrational” or “not spoken.” The worry caused by this secret knowledge was somewhat alleviated by Eudoxus of Cnidos (408-355 BC) when he argued that the basis of reality was a ratio of magnitudes. In effect, Eudoxus made geometry replace arithmetic as the highest mathematical discipline, the foundation of all others. Geometry and arithmetic were hardly even separate disciplines at the time. This change of emphasis allowed Pythagorean teachings about the numeric nature of the universe to continue.

Philosophia et septem artes liberales (Philosophy and the Seven Liberal Arts), as illustrated in the *Hortus deliciarum*. The order of the arts here are: grammar, rhetoric, dialectic, music, arithmetic, geometry, and astronomy. A more detailed study of this image can be found here and here.

The idea that the mathematical disciplines have some orderly relationship between each other is essential for understanding the medieval concept of “quadrivium.” While it is well known that the medieval liberal arts curriculum, at least in its ideal established by Boethius, taught that a student must study both the trivium and quadrivium before progressing to philosophy and theology, the exact nature and rationale for the quadrivium is often less understood. Lists of the arts comprising the quadrivium (arithmetic, geometry, astronomy, and music/harmony) are consistent, but the exact order for these lists can vary. While there is no doubt that sometimes there is truly no rationale for a given order of the mathematical arts, attention to the mathematical art considered the principle or highest can reveal at least three identifiable streams of quadrivial traditions coming from the ancient world (similar to Chenu’s identification of different kinds of Platonism): the Boethian, the Calcidean, and the Capellan. The mathematical art considered “principle” is the one closest to metaphysical reality of the universe and serves as the foundation for all other mathematical disciplines. While the problem of irrational numbers may not have been on the forefront of anyone’s mind in the Middle Ages…it was a closely guarded Pythagorean secret after all…the problem of the principle mathematical art, inherited from Pythagoreanism, was readily available in the source texts.

“Philosophy Presenting the Seven Liberal Arts to Boethius,” about 1460–1470, Coëtivy Master (Henri de Vulcop?), Ms. 42, leaf 2v (91.MS.11.2.verso), Getty Museum Collection.

Boethius (c.480-525) not only established the seven liberal arts as the traditional curriculum for the Middle Ages, but he also wrote treatises on all of the trivium as well as arithmetic, music, and geometry (the latter work is now lost). He, coined the term, “quadrivium” in his attempt to translate the tessares methodoi (four methods) of the Neopythagorean, Nicomachus of Gerasa (c.60-120). Boethius’ own De institutione arithmetica largely draws upon the work of Nicomachus. Modern day history of mathematics textbooks often observe that Nicomachus’ work is one of the first to distinguish arithmetic and geometry as separate disciplines but that the actual quality of the mathematics contains basic errors. Unlike Euclid, Nicomachus doesn’t always give his proofs. Nicomachus presents arithmetic as the principle mathematical art and as a result, so does Boethius. While Boethius was unlikely to have gotten the problem of irrational numbers from Nicomachus because Nicomachus presents arithmetic as the highest mathematical art, Boethius adopts his fourfold division of the mathematical arts along with the belief that arithmetic was the principle mathematical art (De institutio arithmetica 1,1,8).

Image from Boethius’ *De institutione arithmetica* in British Library, Harley MS 549.

In his work on arithmetic, Boethius explains that the order of the quadrivium he offers (music, astronomy, geometry, and arithmetic) both reflects the true nature of the universe and is the proper pedagogical order for the study of mathematics as a preparation for philosophy. Progression through each of the arts trains the mind to move from sense perception to intelligible reality.

Philosophy Instructing Boethius on the Role of God. Coëtivy Master (Henri de Vulcop?), about 1460–1470. Ms. 42, leaf 3 (91.MS.11.3.recto), J. Paul Getty Museum.

This progression of the soul can be seen in the Consolation of Philosophy, where Boethius begins with music and is drawn to philosophy upward by means of astronomy, geometry, and finally arithmetic.

While Boethius’ highly influential order of the quadrivium was adopted by both Cassiodorus and Isidore, Calcidiuswrites very clearly in his commentary on Plato’s Timaeus that geometry is the foundation of all other mathematical arts (Commentum 2.32). His influence throughout the Middle Ages was also extensive. Calcidius’ translation and commentary of Plato’s Timaeus, was one of the only texts of Plato available throughout much of the Middle Ages. Although there were other translations of the Timaeus available, Calcidius’ commentary, as Reydams-Schils has demonstrated, was actually a very good introduction to Platonism as a whole because it was designed to introduce the reader to Platonic doctrine in a pedagogically sequenced way from mathematics to physics and then theology. Throughout the earlier Middle Ages, as Somfai has shown, the commentary was used to teach the quadrivium itself, and earlier versions contained numerous geometrical diagrams. While interest in his geometrical figures appears to fall out of favor in the twelfth century and in newer commentaries on the Timaeus, Nicholas of Cusa in the fourteenth century has both the old Calcidius’ commentaries and the newer commentaries, and geometry clearly plays a major role in his understanding of infinity and kinds of infinity.

Early tenth century manuscript of Calcidius’ Latin translation of Plato’s *Timaeus* from Italy. *Reg. lat. 1308 fols. 21 verso – 22 recto medbio01 NAN.10.*

The third line of quadrivial tradition can be found in Martianus Capella whose Marriage of Philology and Mercury, places music as the highest of the seven liberal arts, the culmination of his entire work. As Michael Masi has observed, this ordering can be found in many visual depictions of the quadrivium, including most famously, the Incarnation Portal at Chartres Cathedral, where arithmetic is paired with geometry as a mathematical study and music with astronomy as a study in harmony. While the complete reasons for this preference are too numerous to identify in a blog, there is a certain kind of Pythagorean logic even here. Music, for Pythagoras and his followers, was thought to be the best evidence for number being at the foundation of the universe. Even the movement of the stars and planets were considered to be one example of many kinds of music in the universe.

Charles Nègre (French, 1820 – 1880), photographer [Chartres Cathedral, Royal Portal (The Incarnation Portal), South Lateral Doorway], 1857. HeliogravureImage: 59.8 × 45.3 cm (23 9/16 × 17 13/16 in.), Sheet: 71.6 × 55.1 cm (28 3/16 × 21 11/16 in.) The J. Paul Getty Museum, Los Angeles, 84.XM.692.4

The stakes for getting the order of the quadrivium right in the Middle Ages may not have risen to the level of murder (although that might make a nice monastic murder mystery written by Umberto Eco, Murder Most Irrational….). And yet, three sources for the quadrivial tradition in the Middle Ages did present the idea that the order of the mathematical arts reflects the most fundamental nature of the universe itself. Furthermore, this fundamental order of the universe has implications for the order of education in the mathematical arts. These stakes, the metaphysical order of the universe and of education, would still have been considered pretty high for most thinkers throughout the Middle Ages.

Lesley-Anne Dyer Williams
Public Humanities Postdoctoral Fellow
Medieval Institute
University of Notre Dame

Further Reading:

Albertson, David. Mathematical Theologies: Nicholas of Cusa and the Legacy of Thierry of Chartres. Oxford University Press, 2014. https://doi.org/10.1093/acprof:oso/9780199989737.001.0001.

Boethius. Boethian Number Theory: A Translation of the “De Institutione Arithmetica” with Introduction and Notes. Translated by Michael Masi. Studies in Classical Antiquity; v. 6. Amsterdam: Rodopi, 1983.

Boethius. The Consolation of Philosophy. Translated by Victor Watts. London: Penguin, 1999.

Burton, David M. The History of Mathematics: An Introduction. Dubuque, Iowa: Wm. C. Brown Publishers, 1988.

Caiazzo, Irene. “Teaching the Quadrivium in the Twelfth-Century Schools.” In A Companion to Twelfth-Century Schools, edited by Cédric Giraud, translated by Ignacio Duran, 88:180–202. Brill’s Companions to the Christian Tradition. Brill, 2019. https://doi.org/10.1163/9789004410138_010.

Calcidius. On Plato’s Timaeus. Dumbarton Oaks Medieval Library 41. Cambridge, Massachusetts; London, England: Harvard University Press, 2016.

Chenu, M. D. Nature, Man, and Society in the Twelfth Century: Essays on New Theological Perspectives in the Latin West. Chicago and London: University of Chicago Press, 1957.

Eco, Umberto. The Name of The Rose. Reprint edition. Boston: HarperVia, 2014.

Evans, Gillian R. “The Influence of Quadrivium Studies in the Eleventh- and Twelfth-Century Schools.” Journal of Medieval History 1, no. 2 (July 1975): 151–64.

Fassler, Margot E. The Virgin of Chartres: Making History through Liturgy and the Arts. Yale University Press, 2010.

Fournier, Michael. “Boethius and the Consolation of the Quadrivium.” Medievalia et Humanistica, no. 34 (2008): 1–21.

Gersh, Stephen. Middle Platonism and Neoplatonism: The Latin Tradition. 2 vols. Notre Dame: University of Notre Dame Press, 1986.

Masi, Michael. “Boethius and the Iconography of the Liberal Arts.” Latomus 33, no. 1 (January 1, 1974): 57–75.

Nicholas of Cusa. Nicholas of Cusa on Learned Ignorance: A Translation and an Appraisal of De Docta Ignorantia. Edited by Jasper Hopkins. Minneapolis: The Arthur Banning Press, 1985.

Oosterhoff, Richard. Making Mathematical Culture: University and Print in the Circle of Lefèvre d’Étaples. Oxford-Warburg Studies. Oxford: University Press, 2018. https://doi.org/10.1093/oso/9780198823520.001.0001.

Reydam-Schils, Gretchen. “Meta-Discourse: Plato’s Timaeus According to Calcidius.” Phronesis 52 (2007): 301–27.

Somfai, Anna. “Calcidius’ Commentary on Plato’s Timaeus and Its Place in the Commentary Tradition: The Concept of Analogia in Text and Diagrams.” Bulletin of the Institute of Classical Studies 47, no. Supplement_83_Part_1 (January 1, 2004): 203–20. https://doi.org/10.1111/j.2041-5370.2004.tb02303.x.

Somfai, Anna. “The Eleventh-Century Shift in the Reception of Plato’s Timaeus and Calcidius’ Commentary.” Journal of the Warburg and Courtauld Institutes 65 (2002): 1–21.

Stahl, William H. “The Quadrivium of Martianus Capella: Its Place in the Intellectual History of Western Europe.” In Arts libéraux et philosophie au moyen âge, 959–67. Actes du IVe Congrès internationl de philosophie médiévale. Montreal Paris, 1969.