Tag: iconography

Posted on

The Quadrivium and the Stakes for Ordering the Mathematical Arts

 Fyodor Bronnikov, Pythagoreans’ Hymn to the Rising Sun, 1869. Oil on canvas.

Legend has it that Pythagoras sentenced the first person to discover irrational numbers, Hippasus of Metapontum (c.530-450 BC), to death. He was tossed overboard a ship to drown. Why? Pythagoras taught that number was the essence and cause of all things, and for Pythagoras and his followers, numbers meant integers. Hippasus’ discovery of irrational numbers appeared to undermine the very core of Pythagoras’ teachings about the numerical nature of the universe. The secret could not get out. Hippasus had to die.

Imaginary engraving of the philosopher Hippasus of Metapontum. From the 1580 book Illustrium philosophorum et sapientum effigies ab eorum numistatibus extractae, by Girolamo Olgiati. Reprinted 1583.

The existence of irrational numbers became a Pythagorean secret. They were called “unutterables” because in Greek, the ratio between two integers was called logos, and so, irrational numbers were called, alogos, which can be translated as either “irrational” or “not spoken.” The worry caused by this secret knowledge was somewhat alleviated by Eudoxus of Cnidos (408-355 BC) when he argued that the basis of reality was a ratio of magnitudes. In effect, Eudoxus made geometry replace arithmetic as the highest mathematical discipline, the foundation of all others. Geometry and arithmetic were hardly even separate disciplines at the time. This change of emphasis allowed Pythagorean teachings about the numeric nature of the universe to continue.

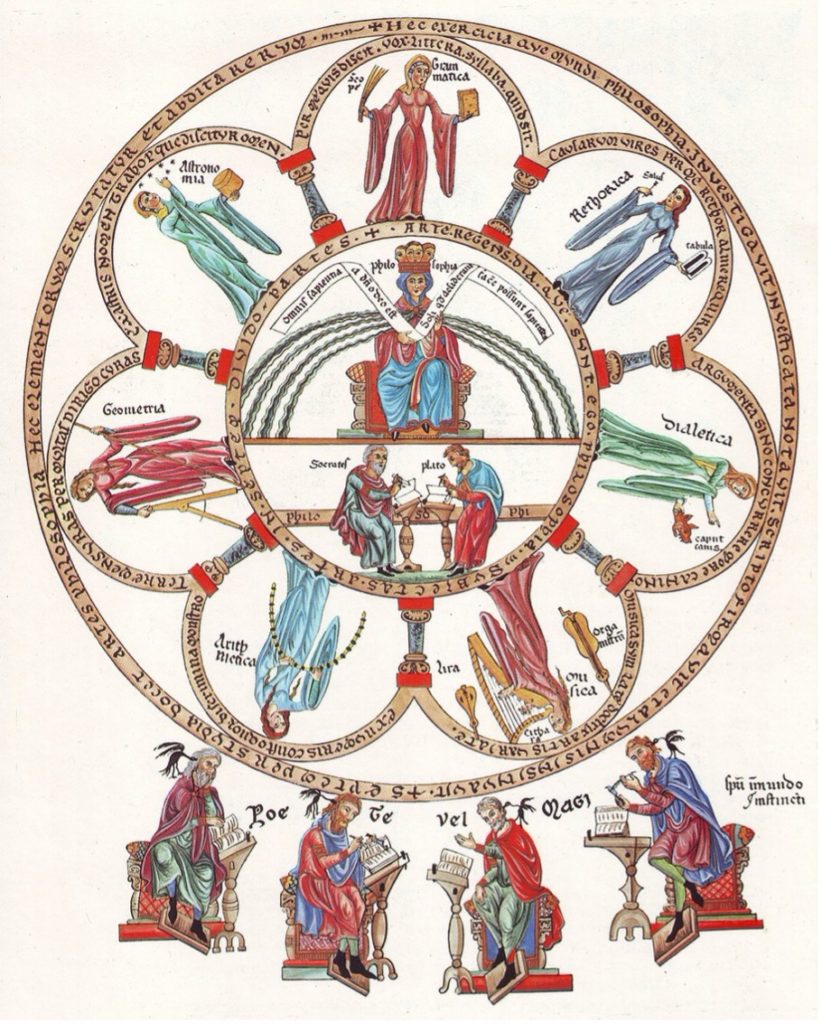
Philosophia et septem artes liberales (Philosophy and the Seven Liberal Arts), as illustrated in the Hortus deliciarum. The order of the arts here are: grammar, rhetoric, dialectic, music, arithmetic, geometry, and astronomy. A more detailed study of this image can be found here and here.

         The idea that the mathematical disciplines have some orderly relationship between each other is essential for understanding the medieval concept of “quadrivium.” While it is well known that the medieval liberal arts curriculum, at least in its ideal established by Boethius, taught that a student must study both the trivium and quadrivium before progressing to philosophy and theology, the exact nature and rationale for the quadrivium is often less understood. Lists of the arts comprising the quadrivium (arithmetic, geometry, astronomy, and music/harmony) are consistent, but the exact order for these lists can vary. While there is no doubt that sometimes there is truly no rationale for a given order of the mathematical arts, attention to the mathematical art considered the principle or highest can reveal at least three identifiable streams of quadrivial traditions coming from the ancient world (similar to Chenu’s identification of different kinds of Platonism): the Boethian, the Calcidean, and the Capellan. The mathematical art considered “principle” is the one closest to metaphysical reality of the universe and serves as the foundation for all other mathematical disciplines. While the problem of irrational numbers may not have been on the forefront of anyone’s mind in the Middle Ages…it was a closely guarded Pythagorean secret after all…the problem of the principle mathematical art, inherited from Pythagoreanism, was readily available in the source texts.

“Philosophy Presenting the Seven Liberal Arts to Boethius,” about 1460–1470, Coëtivy Master (Henri de Vulcop?), Ms. 42, leaf 2v (91.MS.11.2.verso), Getty Museum Collection.

Boethius (c.480-525) not only established the seven liberal arts as the traditional curriculum for the Middle Ages, but he also wrote treatises on all of the trivium as well as arithmetic, music, and geometry (the latter work is now lost).  He, coined the term, “quadrivium” in his attempt to translate the tessares methodoi (four methods) of the Neopythagorean, Nicomachus of Gerasa (c.60-120). Boethius’ own De institutione arithmetica largely draws upon the work of Nicomachus. Modern day history of mathematics textbooks often observe that Nicomachus’ work is one of the first to distinguish arithmetic and geometry as separate disciplines but that the actual quality of the mathematics contains basic errors. Unlike Euclid, Nicomachus doesn’t always give his proofs. Nicomachus presents arithmetic as the principle mathematical art and as a result, so does Boethius. While Boethius was unlikely to have gotten the problem of irrational numbers from Nicomachus because Nicomachus presents arithmetic as the highest mathematical art, Boethius adopts his fourfold division of the mathematical arts along with the belief that arithmetic was the principle mathematical art (De institutio arithmetica 1,1,8).

Image from Boethius’ De institutione arithmetica in British Library, Harley MS 549.

In his work on arithmetic, Boethius explains that the order of the quadrivium he offers (music, astronomy, geometry, and arithmetic) both reflects the true nature of the universe and is the proper pedagogical order for the study of mathematics as a preparation for philosophy. Progression through each of the arts trains the mind to move from sense perception to intelligible reality.

Philosophy Instructing Boethius on the Role of God. Coëtivy Master (Henri de Vulcop?), about 1460–1470. Ms. 42, leaf 3 (91.MS.11.3.recto), J. Paul Getty Museum.

This progression of the soul can be seen in the Consolation of Philosophy, where Boethius begins with music and is drawn to philosophy upward by means of astronomy, geometry, and finally arithmetic.

While Boethius’ highly influential order of the quadrivium was adopted by both Cassiodorus and Isidore, Calcidiuswrites very clearly in his commentary on Plato’s Timaeus that geometry is the foundation of all other mathematical arts (Commentum 2.32). His influence throughout the Middle Ages was also extensive. Calcidius’ translation and commentary of Plato’s Timaeus, was one of the only texts of Plato available throughout much of the Middle Ages. Although there were other translations of the Timaeus available, Calcidius’ commentary, as Reydams-Schils has demonstrated, was actually a very good introduction to Platonism as a whole because it was designed to introduce the reader to Platonic doctrine in a pedagogically sequenced way from mathematics to physics and then theology. Throughout the earlier Middle Ages, as Somfai has shown, the commentary was used to teach the quadrivium itself, and earlier versions contained numerous geometrical diagrams. While interest in his geometrical figures appears to fall out of favor in the twelfth century and in newer commentaries on the Timaeus, Nicholas of Cusa in the fourteenth century has both the old Calcidius’ commentaries and the newer commentaries, and geometry clearly plays a major role in his understanding of infinity and kinds of infinity.

Early tenth century manuscript of Calcidius’ Latin translation of Plato’s Timaeus from Italy. Reg. lat. 1308 fols. 21 verso – 22 recto medbio01 NAN.10.

The third line of quadrivial tradition can be found in Martianus Capella whose Marriage of Philology and Mercury, places music as the highest of the seven liberal arts, the culmination of his entire work. As Michael Masi has observed, this ordering can be found in many visual depictions of the quadrivium, including most famously, the Incarnation Portal at Chartres Cathedral, where arithmetic is paired with geometry as a mathematical study and music with astronomy as a study in harmony. While the complete reasons for this preference are too numerous to identify in a blog, there is a certain kind of Pythagorean logic even here. Music, for Pythagoras and his followers, was thought to be the best evidence for number being at the foundation of the universe. Even the movement of the stars and planets were considered to be one example of many kinds of music in the universe.

Charles Nègre (French, 1820 – 1880), photographer [Chartres Cathedral, Royal Portal (The Incarnation Portal), South Lateral Doorway], 1857. HeliogravureImage: 59.8 × 45.3 cm (23 9/16 × 17 13/16 in.),  Sheet: 71.6 × 55.1 cm (28 3/16 × 21 11/16 in.) The J. Paul Getty Museum, Los Angeles,  84.XM.692.4

The stakes for getting the order of the quadrivium right in the Middle Ages may not have risen to the level of murder (although that might make a nice monastic murder mystery written by Umberto Eco, Murder Most Irrational….). And yet, three sources for the quadrivial tradition in the Middle Ages did present the idea that the order of the mathematical arts reflects the most fundamental nature of the universe itself. Furthermore, this fundamental order of the universe has implications for the order of education in the mathematical arts. These stakes, the metaphysical order of the universe and of education, would still have been considered pretty high for most thinkers throughout the Middle Ages.

Lesley-Anne Dyer Williams is a Professor for Memoria College’s Masters of Arts in Great Books program and graduated with her doctorate from the University of Notre Dame’s Medieval Institute in 2012. She was also the founding director Liberal Arts Guild at LeTourneau University. Her research focuses upon twelfth-century Platonism and poetry, especially Thierry of Chartres and Bernard Silvestris.

Lesley-Anne Dyer Williams
Public Humanities Postdoctoral Fellow
Medieval Institute
University of Notre Dame

Further Reading:

Albertson, David. Mathematical Theologies: Nicholas of Cusa and the Legacy of Thierry of Chartres. Oxford University Press, 2014. https://doi.org/10.1093/acprof:oso/9780199989737.001.0001.

Boethius. Boethian Number Theory: A Translation of the “De Institutione Arithmetica” with Introduction and Notes. Translated by Michael Masi. Studies in Classical Antiquity; v. 6. Amsterdam: Rodopi, 1983.

Boethius. The Consolation of Philosophy. Translated by Victor Watts. London: Penguin, 1999.

Burton, David M. The History of Mathematics: An Introduction. Dubuque, Iowa: Wm. C. Brown Publishers, 1988.

Caiazzo, Irene. “Teaching the Quadrivium in the Twelfth-Century Schools.” In A Companion to Twelfth-Century Schools, edited by Cédric Giraud, translated by Ignacio Duran, 88:180–202. Brill’s Companions to the Christian Tradition. Brill, 2019. https://doi.org/10.1163/9789004410138_010.

Calcidius. On Plato’s Timaeus. Dumbarton Oaks Medieval Library 41. Cambridge, Massachusetts; London, England: Harvard University Press, 2016.

Chenu, M. D. Nature, Man, and Society in the Twelfth Century: Essays on New Theological Perspectives in the Latin West. Chicago and London: University of Chicago Press, 1957.

Eco, Umberto. The Name of The Rose. Reprint edition. Boston: HarperVia, 2014.

Evans, Gillian R. “The Influence of Quadrivium Studies in the Eleventh- and Twelfth-Century Schools.” Journal of Medieval History 1, no. 2 (July 1975): 151–64.

Fassler, Margot E. The Virgin of Chartres: Making History through Liturgy and the Arts. Yale University Press, 2010.

Fournier, Michael. “Boethius and the Consolation of the Quadrivium.” Medievalia et Humanistica, no. 34 (2008): 1–21.

Gersh, Stephen. Middle Platonism and Neoplatonism: The Latin Tradition. 2 vols. Notre Dame: University of Notre Dame Press, 1986.

Martianus Capella. Martianus Capella and the Seven Liberal Arts. Translated by William Harris Stahl, Richard Johnson, and E.L. Burge. Vol. II: The Marriage of Philology and Mercury. 2 vols. Records of Western Civilization 84. Columbia University Press, 1992.

Masi, Michael. “Boethius and the Iconography of the Liberal Arts.” Latomus 33, no. 1 (January 1, 1974): 57–75.

Nicholas of Cusa. Nicholas of Cusa on Learned Ignorance: A Translation and an Appraisal of De Docta Ignorantia. Edited by Jasper Hopkins. Minneapolis: The Arthur Banning Press, 1985.

Oosterhoff, Richard. Making Mathematical Culture: University and Print in the Circle of Lefèvre d’Étaples. Oxford-Warburg Studies. Oxford: University Press, 2018. https://doi.org/10.1093/oso/9780198823520.001.0001.

Reydam-Schils, Gretchen. “Meta-Discourse: Plato’s Timaeus According to Calcidius.” Phronesis 52 (2007): 301–27.

Somfai, Anna. “Calcidius’ Commentary on Plato’s Timaeus and Its Place in the Commentary Tradition: The Concept of Analogia in Text and Diagrams.” Bulletin of the Institute of Classical Studies 47, no. Supplement_83_Part_1 (January 1, 2004): 203–20. https://doi.org/10.1111/j.2041-5370.2004.tb02303.x.

Somfai, Anna. “The Eleventh-Century Shift in the Reception of Plato’s Timaeus and Calcidius’ Commentary.” Journal of the Warburg and Courtauld Institutes 65 (2002): 1–21.

Stahl, William H. “The Quadrivium of Martianus Capella: Its Place in the Intellectual History of Western Europe.” In Arts libéraux et philosophie au moyen âge, 959–67. Actes du IVe Congrès internationl de philosophie médiévale. Montreal Paris, 1969.

Stahl, William Harris, Richard Johnson, and E.L. Burge. Martianus Capella and the Seven Liberal Arts. Vol. I: The Quadrivium of Martianus Capella. 2 vols. Records of Civilization, Sources and Studies 84. New York: Columbia University Press, 1971.

Posted on

Frazetta’s “Death Dealer” and the Question of White Nationalist Iconography at Fort Hood

In 2009, the military base at Fort Hood installed what can only be described as a bizarre sculpture. Sitting outside the headquarters building is a monumental equestrian statue of medieval European fantasy complete with all the expected trappings—chain mail, axe, helmet and a shield here emblazoned with the caltrop of the III Corps United States. As this imposing character looks down with red eyes from his muscled horse, one cannot help but wonder about the figure’s appropriateness within this space. Surely, the statue would better suit an event at Comic-Con than an Army Base.

“Phantom Rider” Statue outside III Corp Headquarters, Fort Hood Texas, 2009.

The sculpture renders Frank Frazetta’s “Death Dealer” a character originally painted in 1973. During his career Frazetta would become famous for creating the cover art for re-printings and pastiches of Robert E. Howard’s Conan the Cimmerian. The infamous, Western barbarian, who spends his time battling Oriental sorcerers and slaughtering black cannibals, played some role in inspiring the “Death Dealer” as suggested by this cover of “Conan the Conqueror” from 1967.

“The Death Dealer,” Frank Frazetta, 1973.
Conan the Conqueror Cover, Frank Frazetta, 1967.

While the original painting obscures the phantom figure’s physical qualities, his weaponry and costume code him as white. The bearded axe and horned helmet recall popular iconography denoting “Viking”[ness], though as some scholars have demonstrated such helmets were largely products of the nineteenth century. Furthermore, his shield bears the reichsadler, the black heraldic eagle employed by the Holy Roman Emperor which has also been used for more contemporary and horrifying purposes. 

Imperial Black Eagle associated with Henry VI from Codex Manesse (c. 1304).
Nazi appropriation of the Imperial Black Eagle in their Reichsadler Symbol (1935-1945).

Admittedly, the visual elements alone do not convey the more problematic elements found in the Conan narratives. As the “Death Dealer” grew in popularity, even becoming adopted as the III Corp mascot in 1986, Frazetta joined author George Silke to create a backstory for his creation in 1987. The novel “Prisoner of the Horned Helmet” begins in a proto-European forest defended by “Gath of Baal” (our Death Dealer). The text, perhaps unsurprisingly, describes “Gath” as a “barbarian” who must defend his homeland from the invading Kitzaaks, a pseudo-Mongol Empire, and their collection of Eastern allies, including the naked and bloodthirsty “Feyan Dervishes.” The cover art here depicts a scene where our hero encounters desert-dwelling “nomads” who have been mutated into dog-faced beings by their continued use of drugs. Such tropes have connections to medieval Latin Christian polemical narrative of Muslims, frequently described as a “race of dogs” or in the case of the Nizari State at Alamut, engaged in the consumption of hashish as part of a perverted “Saracen” practice. Finally, as the “Death Dealer” raises the axe, the artist reveals those corded arms, his previously indeterminable “epidermal” (Heng, 181-184) whiteness is now made manifest.  

Cover of “Prisoner of the Horned Helmet” (The Death Dealer II), Frank Frazetta, 1987.

Evidently, the “Death Dealer” suffers from what Helen Young has previously termed the “Habits of Whiteness” that pervade fantasy literature. As with Tolkien’s and Howard’s work, white bodies and imagined culture is central to this genre. While I do not presume intent on the commissioning of the Fort Hood statue, given the textual narrative, how do we approach this installation of white violence? In fairness, when the III Corps adopted the character they decided to utilize the more politically correct “Phantom Warrior,” perhaps not wishing to glorify “death.” Still, we cannot divorce this sculpture from its racial overtones because of the larger context of artistic and authorial intent. The Army’s own literature manages to perpetuate some of the problems with this imagery, stating that it “represents the heritage and symbol of America’s Armed Corps” and even connects the “Phantom Warrior’s” horse to those employed by William the Conqueror in 1066. Even when devoid of the textual contribution of Frazetta/Silke, the official narrative insists upon a European past.  

By highlighting these issues, I do not mean to attack the Army’s history, though the question of “historical preservation” remains interesting to this conversation. In recent years some discourse has begun to question the public display of Confederate statuary and the naming of military bases for Confederate generals. Opponents of this movement have cried foul, stating that to do so would be to remove American “history.” Of course, these claims are groundless as many of the monuments and bases were erected or named during the early-twentieth century. Yet, even if this were not true, and the icons of Confederacy somehow held an indelible historical value, in what way does an 1980s sword & sorcery construction constitute the pith of American military memory? 

Cover of “Prisoner of the Horned Helmet” (The Death Dealer II), Frank Frazetta, 1987.
“Hood’s Texas Brigade” Monument, Austin TX, 1910.

As we continue to move beyond more obvious examples of racist imagery, perhaps new attention needs to be paid to seemingly neutral renderings which bear all the hallmarks of a white fantasy. Indeed, it is the subtle appellations which allows such narratives to endure. With the escalating number of white nationalist affiliations among military personnel, the public should consider “who does this Warrior speak to and what mythologies does he seek to reinforce?”  

“Phantom Warrior” Statue, Fort Hood, 2009.

Tirumular (Drew) Narayanan
PhD Student in Art History
University of Wisconsin, Madison

Works Cited 

III Corps Centennial Book. September, 13 2018. https://hood.armymwr.com/application/files/8015/4395/7625/III-Corps-Centennial-Book.pdf.

Frank, Roberta. “The Invention of the Viking Horned Helmet.” International Scandinavian and Medieval Studies in memory of Gerd Wolfgang Weber (2000): 199-208.

Higgs Strickland, Debra. “Monstrosity and Race in the Late Middle Ages.” In The Ashgate Research Companion to Monsters and The Monstrous. Edited by Asa Simon Mittman with Peter J. Dendle, 365-386. New York: Routledge, 2016.

Heng, Geraldine. The Invention of Race in the European Middle Ages. Cambridge: Cambridge University Press, 2018. 

Young, Helen. Race and Popular Fantasy Literature: Habits of Whiteness. New York: Routledge, 2016.  

Brooks, Lecia. “SPLC Testifies Before Congress on Alarming Incidents of White Supremacy in the Military.” Last modified February 11, 2016. https://www.splcenter.org/news/2020/02/11/splc-testifies-congress-alarming-incidents-white-supremacy-military.

Risen, James. “Why is the Army Still Honoring Confederate Generals?” The Intercept. Last Modified October 6,2019. https://theintercept.com/2019/10/06/army-bases-confederate-names/.

Posted on

Theodore Metochites’s “Lament on Human Life,” A Later Byzantine Perspective on the Anxiety of “Instability”

Cameo, Constantine the Great and the Tyche of Constantinople wearing her turreted crown, sardonyx, 4th century. Image: The State Hermitage Museum.

Alas, alas, Life, you monstrous thing replete with every kind of misfor­tune, breeder of misfortune, theater of misfortune, and most of all of insta­bility!

– Theodore Metochites (SG 27.1.1)

In the wake of COVID-19’s spread into a pandemic, the world has fallen into a state of collective anxiety. As a historian, I find that in such challenging times, my inclination is to look to the past. At this moment when we all contend with isolation, grief, scarcity, and the fear of contagion, we may find some solace and insight by exploring the ways in which humanity has previously coped with such feelings of uncertainty. Much of my work this year at the Medieval Institute has focused on the Byzantine statesman and polymath, Theodore Metochites (1270–1332), and his theorization of memory as expressed in his scholarship and in the iconographic program of the Chora Monastery, the renovation of which he oversaw and endowed (c. 1316–1321). No stranger to turmoil in his own life, Metochites also reflects at length on the idea of “instability” (astasia) in his writings. Several chapters of his encyclopedic work, the Semeioseis gnomikai, or “Sententious Notes,” address this recurring theme as the author himself works through the notion of uncontrollable change and fickle Fortune.

Metochites’s observations on fate draw from his own experiences of the ebb and flow of politics. In 1283, Emperor Andronikos II Palaiologos (1259/60–1331, r. 1282–1328) ousted Metochites’s father, George, from Constantinople for his opposing policies, and, at thirteen years old, young Theodore accompanied his father into exile. While in Asia Minor, Metochites dedicated himself to his education and, by 1290, as he writes, “the winds shift[ed] from one direction to the opposite” (SG 28.3.5). The same Andronikos II, having learned of Metochites’s reputation for erudition, called him to serve in the imperial court, where he achieved the high rank of Megas Logothetes, or prime minister. He takes care to acknowledge that his change in fortune was an external one, beyond his control: “the difficulties of my life suddenly and perhaps unexpectedly changed … although I had in no way changed, in the way it usually happens among men” (SG 28.3.4–5).

In a rather pessimistic frame of mind, he continues by pointing out that even in the grace of good fortune, the popular saying rings true: “it is impossible to find anyone living a life free of sorrows” (Hult 13). Metochites tells us that as his position and fortune increased, he felt steadily more burdened by state affairs. He writes that it was “extremely distressing … to be personally in charge of conducting and somehow administering the shipwreck of Roman world power, and many times, when I could see no way out in my thoughts and I completely lost hope, I prayed that this seeming blessing and favor from Fortune would not have fallen to my lot” (SG 28.5.4 and 6.4–5). Good fortune brings with it no guarantee of happiness.

Theodore Metochites presenting his foundation to Christ, Esonarthex, Lunette above eastern door, Chora Monastery, c. 1316–1321, Istanbul, Turkey. Image: Brad Hostetler.

In the same essay, Metochites draws an evocative comparison between the whims of political fortune and sudden changes in health:

No, we can see even the strongest and those with bodies in excel­lent condition in absolutely every respect easily lose their physical strength and confidence, struck down now and then by a chance occurrence, some­thing which others who are perhaps not equally well-endowed with bodily strength have managed to escape. And we see the man who yesterday was standing firm, indeed, who was for a long time undefeated by any kind of bodily misfortune, now lying on his back and suffering some malaise in his body, that had, until now, been extremely vigorous, or having lost all his health and now experiencing numerous difficult changes, living with all kinds of sickness—he who for many years seemed completely impervious to the vicissitudes of the body. (SG 28.2.1–3)

As easily and as quickly as the body succumbs to illness, so too do rapid shifts in fate occur in all other contexts of life, from wealth to family and career. This association amplifies points set forth in the preceding chapter of the Semeiosis. In his “Lament of human life,” Metochites opens with a description of the two sides of human reaction to fortune’s instability. Those currently experiencing good fortune constantly live in expectation and anxiety of worse things to come, while those who are struggling live with the hope of better days. With the flip of a coin (or “turn of the ostrakon” in ancient Greek and Byzantine parlance), the greatest wealth yields to poverty, robust health deteriorates to languid weakness. He goes on to say, however, that instability, though unforeseeable, should be expected. Reacting to the assertion that change is abrupt, he argues the opposite: “I unhesitatingly add that [it has been coming] for a long time, indeed from the beginning” (SG 27.2.5). Metochites follows the concept of “universal flux” put forth by Heraclitus, and elaborates on the maxim still referenced today, “the only thing constant is change” (cf. SG 29.2.1–7). He concludes that it is wisest to acknowledge, either through personal experience or observation of others, that life is inconstant; with this in mind, one must “live not unprepared for the likelihood of good things turning utterly bad and so live better” (SG 27.2.7).

Toward the end of his life, Metochites found reason to affirm his comments on misfortune’s predictably unpredictable appearance. In the margins of Paris gr. 2003, pictured below, we find a retrospective remark written in light of his second exile from the capital in 1328. Following the ascendance of Andronikos III to the throne after a long period of civil war, Metochites was forced to reside in Didymoteicho (today in northeastern Greece) before returning to take monastic vows in his foundation of the Chora two years later. To the earlier words of his “lament,” he declares, “I myself have suffered this as I foretold” (Hult xv).

Theodore Metochites, “A Lament on Human Life,” Paris gr. 2003, f. 49r (56r), 15th century. Image: Bibliothèque nationale de France.

Metochites’s essay further deliberates on the saying that, “because of death we are living in a city without walls.” The original Epicurean context of this adage emphasized the indefensibility of the human body and inevitability of death. Building on this metaphorical meaning, Metochites states that we are, “like people living in a city without walls also because of the changes from prosperity to adversity, from perfect health to sickness, and on the whole from good fortune to bad …” (SG 27.2.1–6). Though he was writing in a much different cultural context than ours today, we might bring a critical eye to Metochites’s musings as a way of contemplating COVID-19-era insecurity. The rapid spread of illness threatens to render our “city walls” – the infrastructure of our healthcare and economy – susceptible to collapse. Anxiety arises from the permeability of these defenses. With an understanding that none of us is immune to “the attacks and sieges of Chance,” we can reassess the way we conceptualize and respond to drastically new realities.

While Metochites reflects on Fortune from the viewpoint of a privileged Byzantine elite, the current pandemic has laid bare the shared, but uneven vulnerability to “fate” in our society. In many ways, the virus’s dismantling of our “city walls” has lead to an exposure of inequality, and the situation thus demands that we reconstruct societal concepts of space and community. As we grasp to control contagion through worldwide self-isolation, the “fate” of the individual is inextricably tied to the many. Risk and instability, however, are not experienced equitably. Indeed, the necessity of social distancing has demonstrated just how few “walls” had been erected to fortify the health and well-being of all in the first place. Metochites reflected on his personal experiences to assess the nature of fate and life’s inconstancy. When this crisis is behind us, perhaps we will not forget the diversity of individual experiences in the face of uncertainty. Only then might we rebuild a fortress of collective action better equipped to sustain the many against the next unpredictable, inevitable turn of fate.

Nicole Paxton Sullo
2019–20 Byzantine Studies Postdoctoral Fellow at the Medieval Institute
Ph.D., History of Art, Yale University (2020)

All translations based on:

Karin Hult, ed. and trans., Theodore Metochites on the Human Condition and the Decline of Rome: Semeioseis gnomikai 27–60, Studia Graeca et Latina Gothoburgensia 70 (Gothenburg: Kriterium, 2016). DOI: 10.21524/kriterium.4.